题目内容
命题p:函数f(x)=ax3+ax2+x既有极大值又有极小值;命题q:抛物线x2=2ay(a≠0)的准线与圆C:(x-2)2+(y+2)2=1相交.
(1)若“p或q”为真命题,求实数a的取值范围;
(2)若“p或q”为真命题,“p且q”为假命题,求实数a的取值范围.
(1)若“p或q”为真命题,求实数a的取值范围;
(2)若“p或q”为真命题,“p且q”为假命题,求实数a的取值范围.
考点:复合命题的真假,利用导数研究函数的极值,抛物线的简单性质
专题:常规题型,简易逻辑
分析:首先考虑p,q为真时的等价结论:函数f(x)=x3+ax2+ax-a既有极大值又有极小值说明导函数图象与x轴有两个不同的交点,即判别式>0;又抛物线x2=2ay(a≠0)的准线与圆C:(x-2)2+(y+2)2=1相交即圆心C(2,-2)到抛物线x2=2ay,(a≠0)的准线:y=-
的距离小于1,再由真值表列出不等式组求出a的范围.
| a |
| 2 |
解答:
解:命题p真:函数f(x)既有极大值又有极小值,
即:f'(x)=0有两个不等的实根,
则f'(x)=3ax2+2ax+1=0有两个不等的实根,
∴
则:a>3或a<0…(3分)
命题q真:圆心C(2,-2)到抛物线x2=2ay,(a≠0)的准线:y=-
的距离小于1,
即|-
+2|<1
∴2<a<6
(1)若“p或q”为真命题,
∴p或q中有真命题,
∴a>2或a<0;
即:实数a的取值范围为(2,+∞)∪(-∞,0)…(9分)
(2)若“p或q”为真命题,“p且q”为假命题,
则:p,q一真一假.
当p假q真时,有
即2<a≤3;
当p真q假时,有
,解得:a<0或a≥6.
∴实数a的取值范围为(-∞,0)∪(2,3]∪[6,+∞)…(12分)
即:f'(x)=0有两个不等的实根,
则f'(x)=3ax2+2ax+1=0有两个不等的实根,
∴
|
命题q真:圆心C(2,-2)到抛物线x2=2ay,(a≠0)的准线:y=-
| a |
| 2 |
即|-
| a |
| 2 |
∴2<a<6
(1)若“p或q”为真命题,
∴p或q中有真命题,
∴a>2或a<0;
即:实数a的取值范围为(2,+∞)∪(-∞,0)…(9分)
(2)若“p或q”为真命题,“p且q”为假命题,
则:p,q一真一假.
当p假q真时,有
|
当p真q假时,有
|
∴实数a的取值范围为(-∞,0)∪(2,3]∪[6,+∞)…(12分)
点评:本题考查的知识点是命题的真假判断与应用,利用导数研究函数的极值,在确定命题p,q为真命题时,求参数a的取值范围,难度比较大,也容易出错.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
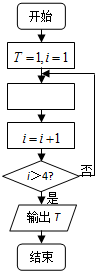
如图所示的程序框图,若执行运算1×
×
×
×
,则在空白执行框中,应该填入( )
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |

| A、T=T•(i+1) | ||
| B、T=T•i | ||
C、T=T•
| ||
D、T=T•
|
函数f(x)=Msinωx(ω>0),在区间[a,b]上是增函数,且f(a)=-M,f(b)=M,则函数f(x)=Mcosωx在区间[a,b]上( )
| A、是增函数 |
| B、是减函数 |
| C、可以取得最大值M |
| D、可以取得最小值-M |
 如图所示扇形AOB,半径为2,∠AOB=
如图所示扇形AOB,半径为2,∠AOB= 如图,已知二次函数为y=x2,求抛物线与x=1和x轴组成的封闭图形的面积.
如图,已知二次函数为y=x2,求抛物线与x=1和x轴组成的封闭图形的面积.