题目内容
1.若正四棱锥的侧棱长为$\sqrt{3}$,侧面与底面所成的角是45°,则该正四棱锥的体积是( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{4\sqrt{2}}{3}$ |
分析 作出棱锥的高与斜高,得出侧面与底面所成角的平面角,利用勾股定理列方程解出底面边长,代入体积公式计算.
解答 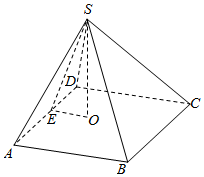 解:过棱锥定点S作SE⊥AD,SO⊥平面ABCD,则E为AD的中点,O为正方形ABCD的中心.
解:过棱锥定点S作SE⊥AD,SO⊥平面ABCD,则E为AD的中点,O为正方形ABCD的中心.
连结OE,则∠SEO为侧面SAD与底面ABCD所成角的平面角,即∠SEO=45°.
设正四棱锥的底面边长为a,则AE=OE=SO=$\frac{a}{2}$,
∴SE=$\sqrt{2}EO$=$\frac{\sqrt{2}}{2}a$.
在Rt△SAE中,∵SA2=AE2+SE2,
∴3=$\frac{{a}^{2}}{4}+\frac{{a}^{2}}{2}$,解得a=2.
∴SO=1,
∴棱锥的体积V=$\frac{1}{3}{S}_{正方形ABCD}•SO$=$\frac{1}{3}×{2}^{2}×1=\frac{4}{3}$.
故选B.
点评 本题考查了正棱锥的结构特征,体积计算,属于基础题.

练习册系列答案
相关题目
11.已知O为坐标原点,F1,F2是双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点,P是双曲线右支上一点,PM为∠F1PF2的角平分线,过F1作PM的垂线交PM于点M,则|OM|的长度为( )
| A. | a | B. | b | C. | $\frac{a}{2}$ | D. | $\frac{b}{2}$ |
12.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一条渐近线方程为y=$\frac{\sqrt{7}}{3}$x,它的一个顶点到较近焦点的距离为1,则双曲线方程为( )
| A. | $\frac{{x}^{2}}{7}$-$\frac{{y}^{2}}{9}$=1 | B. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{7}$=1 | D. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 |
9.已知点P在双曲线$\frac{x^2}{a^2}-\frac{y^2}{16}$=1的右支上,F为双曲线的左焦点,Q为线段PF的中点,O为坐标原点.若|OQ|的最小值为1,则双曲线的离心率为( )
| A. | $\frac{17}{15}$ | B. | $\frac{15}{17}$ | C. | $\frac{3}{5}$ | D. | $\frac{5}{3}$ |
16.设点P为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$上一点,F1,F2分别是左右焦点,I是△PF1F2的内心,若△IPF1,△IPF2,△IF1F2的面积S1,S2,S3满足2(S1-S2)=S3,则双曲线的离心率为( )
| A. | 2 | B. | $\sqrt{3}$ | C. | 4 | D. | $\sqrt{2}$ |
6.一个六棱柱的底面是正六边形,侧棱垂直于底面,所有棱的长都为1,顶点都在同一个球面上,则该球的体积为( )
| A. | 20π | B. | $\frac{{20\sqrt{5}π}}{3}$ | C. | 5π | D. | $\frac{{5\sqrt{5}π}}{6}$ |
13.过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的一个焦点F作双曲线的一条渐近线的垂线,若垂线的延长线与y轴的交点坐标为$(0\;,\;\;\frac{c}{2})$,则此双曲线的离心率是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
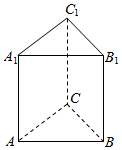 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠BAC=90°,AB=AC=2,AA1=4
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠BAC=90°,AB=AC=2,AA1=4