题目内容
16.设点P为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$上一点,F1,F2分别是左右焦点,I是△PF1F2的内心,若△IPF1,△IPF2,△IF1F2的面积S1,S2,S3满足2(S1-S2)=S3,则双曲线的离心率为( )| A. | 2 | B. | $\sqrt{3}$ | C. | 4 | D. | $\sqrt{2}$ |
分析 先根据题意作出示意图,如图所示,利用平面几何的知识利用三角形面积公式,代入已知式2(S1-S2)=S3,化简可得|PF1|-|PF2|=$\frac{1}{2}$|F1F2|,再结合双曲线的定义与离心率的公式,可求出此双曲线的离心率.
解答 解:如图,设圆I与△PF1F2的三边F1F2、PF1
PF2分别相切于点E、F、G,连接IE、IF、IG,
则IE⊥F1F2,IF⊥PF1,IG⊥PF2,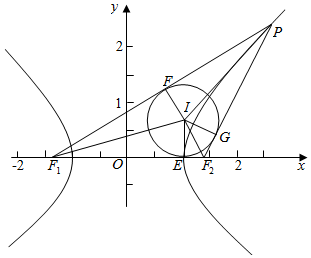
它们分别是△IF1F2,△IPF1,△IPF2的高,
∴S1=$\frac{1}{2}$|PF1|•|IF|=$\frac{1}{2}$|PF1|r,
S2=$\frac{1}{2}$|PF2|•|IG|=$\frac{1}{2}$|PF2|r,
S3=$\frac{1}{2}$|F1F2|•|IE|=$\frac{1}{2}$|F1F2|r,
其中r是△PF1F2的内切圆的半径.
∵S1-S2=$\frac{1}{2}$S3,
∴$\frac{r}{2}$|PF1|-$\frac{r}{2}$|PF2|=$\frac{r}{4}$|F1F2|,
两边约去$\frac{r}{2}$得:|PF1|-|PF2|=$\frac{1}{2}$|F1F2|,
根据双曲线定义,得|PF1|-|PF2|=2a,|F1F2|=2c,
∴2a=c⇒离心率为e=$\frac{c}{a}$=2.
故选:A.
点评 本题将三角形的内切圆放入到双曲线当中,用来求双曲线的离心率,着重考查了双曲线的基本性质、三角形内切圆的性质和面积计算公式等知识点,属于中档题.

练习册系列答案
相关题目
4.已知l是双曲线C:$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{4}$=1的一条渐近线,P是l上的一点,F1,F2是C的两个焦点,若$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0,则P到x轴的距离为( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $\frac{2\sqrt{6}}{3}$ |
11.已知点F1,F2为双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左,右焦点,点P在双曲线C的右支上,且满足|PF2|=|F1F2|,∠F1F2P=120°,则双曲线的离心率为( )
| A. | $\frac{{\sqrt{3}+1}}{2}$ | B. | $\frac{{\sqrt{5}+1}}{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
1.若正四棱锥的侧棱长为$\sqrt{3}$,侧面与底面所成的角是45°,则该正四棱锥的体积是( )
| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{4\sqrt{2}}{3}$ |
8.若集合A={x|1<x<3},B={x|x>2},则A∩B=( )
| A. | {x|2<x<3} | B. | {x|1<x<3} | C. | {x|1<x<2} | D. | {x|x>1} |
5.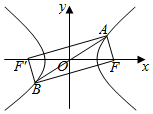 如图,已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$上有一点A,它关于原点的对称点为B,点F为双曲线的右焦点,且满足AF⊥BF,设∠ABF=α,且$α∈[{\frac{π}{12},\frac{π}{6}}]$,则该双曲线离心率e的取值范围为( )
如图,已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$上有一点A,它关于原点的对称点为B,点F为双曲线的右焦点,且满足AF⊥BF,设∠ABF=α,且$α∈[{\frac{π}{12},\frac{π}{6}}]$,则该双曲线离心率e的取值范围为( )
 如图,已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$上有一点A,它关于原点的对称点为B,点F为双曲线的右焦点,且满足AF⊥BF,设∠ABF=α,且$α∈[{\frac{π}{12},\frac{π}{6}}]$,则该双曲线离心率e的取值范围为( )
如图,已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$上有一点A,它关于原点的对称点为B,点F为双曲线的右焦点,且满足AF⊥BF,设∠ABF=α,且$α∈[{\frac{π}{12},\frac{π}{6}}]$,则该双曲线离心率e的取值范围为( )| A. | $[{\sqrt{2},\sqrt{3}+1}]$ | B. | $[{\sqrt{3},2+\sqrt{3}}]$ | C. | $[{\sqrt{2},2+\sqrt{3}}]$ | D. | $[{\sqrt{3},\sqrt{3}+1}]$ |
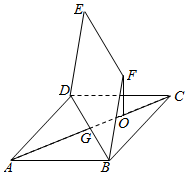 如图,正方形ABCD的边长为2$\sqrt{2}$,四边形BDEF是平行四边形,BD与AC交于点G,O为GC的中点,且FO⊥平面ABCD,FO=$\sqrt{3}$.
如图,正方形ABCD的边长为2$\sqrt{2}$,四边形BDEF是平行四边形,BD与AC交于点G,O为GC的中点,且FO⊥平面ABCD,FO=$\sqrt{3}$.