题目内容
13．过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$（a＞0，b＞0）的一个焦点F作双曲线的一条渐近线的垂线，若垂线的延长线与y轴的交点坐标为$（0\;，\;\;\frac{c}{2}）$，则此双曲线的离心率是（ ）| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | 2 | D． | $\sqrt{5}$ |
分析 设双曲线的一个焦点F（c，0），一条渐近线方程为y=$\frac{b}{a}$x，运用两直线垂直的条件：斜率之积为-1，可得b=2a，再由离心率公式计算即可得到所求值．
解答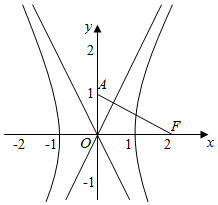 
解：设双曲线的一个焦点F（c，0），一条渐近线方程为y=$\frac{b}{a}$x，
∵垂线的延长线与y轴的交点坐标为A$（0\;，\;\;\frac{c}{2}）$，
∴由两直线垂直的条件：斜率之积为-1，可得$\frac{b}{a}$•$\frac{\frac{c}{2}-0}{-c}$=-1，
即b=2a，
则c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{5}$a，
即有e=$\frac{c}{a}$=$\sqrt{5}$．
故选：D
点评 本题考查双曲线的离心率的求法，注意运用双曲线的焦点和渐近线方程、两直线垂直的条件以及离心率公式，考查运算能力．
练习册系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
4．已知l是双曲线C：$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{4}$=1的一条渐近线，P是l上的一点，F1，F2是C的两个焦点，若$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0，则P到x轴的距离为（ ）
| A． | $\frac{2\sqrt{3}}{3}$ | B． | $\sqrt{2}$ | C． | 2 | D． | $\frac{2\sqrt{6}}{3}$ |
1．若正四棱锥的侧棱长为$\sqrt{3}$，侧面与底面所成的角是45°，则该正四棱锥的体积是（ ）
| A． | $\frac{2}{3}$ | B． | $\frac{4}{3}$ | C． | $\frac{2\sqrt{2}}{3}$ | D． | $\frac{4\sqrt{2}}{3}$ |
8．若集合A={x|1＜x＜3}，B={x|x＞2}，则A∩B=（ ）
| A． | {x|2＜x＜3} | B． | {x|1＜x＜3} | C． | {x|1＜x＜2} | D． | {x|x＞1} |
5．
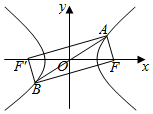如图，已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$上有一点A，它关于原点的对称点为B，点F为双曲线的右焦点，且满足AF⊥BF，设∠ABF=α，且$α∈[{\frac{π}{12}，\frac{π}{6}}]$，则该双曲线离心率e的取值范围为（ ）
如图，已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$上有一点A，它关于原点的对称点为B，点F为双曲线的右焦点，且满足AF⊥BF，设∠ABF=α，且$α∈[{\frac{π}{12}，\frac{π}{6}}]$，则该双曲线离心率e的取值范围为（ ）| A． | $[{\sqrt{2}，\sqrt{3}+1}]$ | B． | $[{\sqrt{3}，2+\sqrt{3}}]$ | C． | $[{\sqrt{2}，2+\sqrt{3}}]$ | D． | $[{\sqrt{3}，\sqrt{3}+1}]$ |
3．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的两条渐近线与抛物线y2=4x的准线分别交于A，B两点，O为坐标原点，若双曲线的离心率为2，则△AOB的面积为（ ）
| A． | 2 | B． | 2$\sqrt{3}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\sqrt{3}$ |