题目内容
若x∈R，ax2+4x+a≥-2x2+1恒成立，则实数a的取值范围是（ ）
| A、-2＜a≤2 |
| B、a≥2 |
| C、a＞-2 |
| D、a≤-3或a≥2 |
考点：全称命题
专题：不等式的解法及应用
分析：根据不等式恒成立的条件，即可求出a的取范围．
解答：
解：不等式ax2+4x+a≥-2x2+1等价为（a+2）x2+4x+a-1≥0恒成立．
若a=-2，不等式等价为4x-3≥0，即x≥
，此时不满足条件．
若a≠-2，要使不等式恒成立，
则满足
，
即
，
∴
，
∴a≥2，
故选：B．
若a=-2，不等式等价为4x-3≥0，即x≥
| 3 |
| 4 |
若a≠-2，要使不等式恒成立，
则满足
|
即
|
∴
|
∴a≥2，
故选：B．
点评：本题主要考查不等式恒成立问题，利用一元二次不等式恒成立的条件是解决本题的根据，注意要进行分类讨论．
练习册系列答案
相关题目
已知向量
≠
，
，
≠
，对任意t∈R，恒有|
+t
|≥|
+
|，则（ ）
| a |
| e |
| a |
| e |
| 0 |
| a |
| e |
| a |
| e |
A、（
| ||||||
B、（
| ||||||
C、
| ||||||
D、|
|
若m＞1，则方程
+
=1表示（ ）
| x2 |
| m-1 |
| y2 |
| m2-1 |
| A、焦点在x轴上的椭圆 |
| B、焦点在y轴上的椭圆 |
| C、焦点在x轴上的双曲线 |
| D、焦点在y轴上的双曲线 |
若直线ax+y+1=0与圆x2+y2-2x=0相切，则a的值为（ ）
| A、±1 | B、±2 | C、-1 | D、0 |
过双曲线
-
=1的左焦点，且斜率为1的直线l恰与双曲线的左支有两个不同交点，则双曲线的离心率的取值范围为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、e＞2 | ||
B、1＜e＜
| ||
C、e＞
| ||
| D、1＜e＜2 |
已知命题P：?x∈R，x2+2ax+a≤0．若命题P是假命题，则实数a的取值范围是（ ）
| A、（0，1） |
| B、（-∞，0）∪（1，+∞） |
| C、[0，1] |
| D、（-∞，0）∪[1，+∞） |
若抛物线y2=2px，（p＞0）上一点P（2，y0）到其准线的距离为4，则抛物线的标准方程为（ ）
| A、y2=4x |
| B、y2=6x |
| C、y2=8x |
| D、y2=10x |
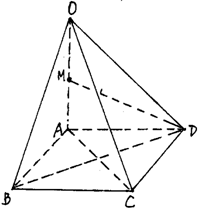如图，在四棱锥O-ABCD中，底面ABCD是边长为1的正方形，OA⊥底面ABCD，OA=2，M为OA中点．