题目内容
对某电子元件进行寿命追踪调查,所得情况如频率分布直方图.

(1)图中纵坐标y0处刻度不清,根据图表所提供的数据还原y0;
(2)根据图表的数据按分层抽样,抽取20个元件,寿命为100~300之间的应抽取几个;
(3)从(2)中抽出的寿命落在100~300之间的元件中任取2个元件,求事件“恰好有一个寿命为100~200,一个寿命为200~300”的概率.

(1)图中纵坐标y0处刻度不清,根据图表所提供的数据还原y0;
(2)根据图表的数据按分层抽样,抽取20个元件,寿命为100~300之间的应抽取几个;
(3)从(2)中抽出的寿命落在100~300之间的元件中任取2个元件,求事件“恰好有一个寿命为100~200,一个寿命为200~300”的概率.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:(1)根据图标可得0.001×100+2y0×100+0.002×100+0.004×100=1,从而可求出y0的值.
(2)设在寿命为100~300之间的应抽取x个,根据分层抽样即可得出x的值.
(3)由(2)知寿命落在100~200之间的元件有2个,落在200~300之间的元件有3个.根据题意可知基本事件有10个,恰好有一个寿命为100~200,一个寿命为200~300的事件有6个,进而得出概率.
(2)设在寿命为100~300之间的应抽取x个,根据分层抽样即可得出x的值.
(3)由(2)知寿命落在100~200之间的元件有2个,落在200~300之间的元件有3个.根据题意可知基本事件有10个,恰好有一个寿命为100~200,一个寿命为200~300的事件有6个,进而得出概率.
解答:
解(1)根据题意:0.001×100+2y0×100+0.002×100+0.004×100=1
解得y0=0.0015.
(2)设在寿命为100~300之间的应抽取x个,根据分层抽样有:
=(0.001+0.0015)×100.
解得:x=5.
所以应在寿命为100~300之间的应抽取5个.
(3)记“恰好有一个寿命为100~200,一个寿命为200~300”为事件A,
由(2)知寿命落在100~200之间的元件有2个分别记a1,a2,
落在200~300之间的元件有3个分别记为:b1,b2,b3,
从中任取2个球,有如下基本事件:
(a1,a2),(a1,b1),(a1,b2),(a1,b3),(a2,b1),(a2,b2),(a2,b3),(b1,b2),(b1,b3),(b2,b3).
共有10个基本事件.
事件A“恰好有一个寿命为100~200,一个寿命为200~300”有:
(a1,b1),(a1,b2),(a1,b3),(a2,b1),(a2,b2),(a2,b3),共有6个基本事件.
∴P(A)=
=
.
∴事件“恰好有一个寿命为100~200,另一个寿命为200~300”的概率为
.
解得y0=0.0015.
(2)设在寿命为100~300之间的应抽取x个,根据分层抽样有:
| x |
| 20 |
解得:x=5.
所以应在寿命为100~300之间的应抽取5个.
(3)记“恰好有一个寿命为100~200,一个寿命为200~300”为事件A,
由(2)知寿命落在100~200之间的元件有2个分别记a1,a2,
落在200~300之间的元件有3个分别记为:b1,b2,b3,
从中任取2个球,有如下基本事件:
(a1,a2),(a1,b1),(a1,b2),(a1,b3),(a2,b1),(a2,b2),(a2,b3),(b1,b2),(b1,b3),(b2,b3).
共有10个基本事件.
事件A“恰好有一个寿命为100~200,一个寿命为200~300”有:
(a1,b1),(a1,b2),(a1,b3),(a2,b1),(a2,b2),(a2,b3),共有6个基本事件.
∴P(A)=
| 6 |
| 10 |
| 3 |
| 5 |
∴事件“恰好有一个寿命为100~200,另一个寿命为200~300”的概率为
| 3 |
| 5 |
点评:本题考查频率分布直方图的应用,分层抽样以及古典概型的概率公式等知识的综合应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
复数z=1+i,则
+
对应的点所在的象限为( )
| 1 |
| z |
. |
| z |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
等差数列x1,x2,x3…x9的公差为1,随机变量ξ等可能的取值x1,x2,x3…x9,则方差D(ξ)为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
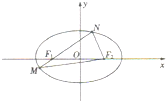 如图,椭圆E:
如图,椭圆E: