题目内容
函数y=
的值域是 .
| 2x |
| x2+x+1 |
考点:函数的值域
专题:函数的性质及应用
分析:当x=0时,可得y=0;当x≠0时,y=
,令t=x+
,x≠0,由“对号函数”的性质可得t的范围,由不等式的性质可得y的范围.
| 2 | ||
x+1+
|
| 1 |
| x |
解答:
解:当x=0时,可得y=0;
当x≠0时,分子分母同除以x可得y=
,
令t=x+
,x≠0,由“对号函数”的性质
易得t∈(-∞,-2]∪[2,+∞),
∴x+
+1∈(-∞,-1]∪[3,+∞),
∴
∈[-2,0)∪(0,
],即y∈[-2,0)∪(0,
],
综上可得函数的值域为:[-2,
],
故答案为:[-2,
]
当x≠0时,分子分母同除以x可得y=
| 2 | ||
x+1+
|
令t=x+
| 1 |
| x |
易得t∈(-∞,-2]∪[2,+∞),
∴x+
| 1 |
| x |
∴
| 2 | ||
x+1+
|
| 2 |
| 3 |
| 2 |
| 3 |
综上可得函数的值域为:[-2,
| 2 |
| 3 |
故答案为:[-2,
| 2 |
| 3 |
点评:本题考查函数的值域,涉及分类讨论的思想和“对号函数”的单调性和值域,属基础题.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
下列四个命题中,正确的是( )
| A、“若xy=0,则x=0且y=0”的逆否命题 |
| B、“若ac2>bc2则a>b”的逆命题 |
| C、若“m>2,则不等式x2-2x+m>0的解集为R” |
| D、“正方形是菱形”的否命题 |


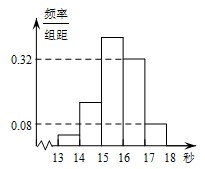 已知某年级1000名学生的百米跑成绩全部介于13秒与18秒之间,为了了解学生的百米跑成绩情况,随机抽取了若干学生的百米跑成绩,并按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为1:4:10,且第二组的频数为8.
已知某年级1000名学生的百米跑成绩全部介于13秒与18秒之间,为了了解学生的百米跑成绩情况,随机抽取了若干学生的百米跑成绩,并按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为1:4:10,且第二组的频数为8.