题目内容
已知点A（2，3），B（5，4），C（7，10），若
=
+λ•
(λ∈R)，
（1）若点P在第一、三象限的角平分线上，求λ的值；
（2）若点P在第三象限内，求λ的取值范围．
| AP |
| AB |
| AC |
（1）若点P在第一、三象限的角平分线上，求λ的值；
（2）若点P在第三象限内，求λ的取值范围．
考点：向量加减混合运算及其几何意义
专题：平面向量及应用
分析：（1）由于点P在第一、三象限的角平分线上，可设P（a，a）．利用向量的坐标运算
=
+λ•
(λ∈R)，和向量相等即可得出．
（2）设P（x，y），利用向量的坐标运算和向量相等及点P在第三象限，即可得出．
| AP |
| AB |
| AC |
（2）设P（x，y），利用向量的坐标运算和向量相等及点P在第三象限，即可得出．
解答：
解：（1）∵点P在第一、三象限的角平分线上，∴可设P（a，a）．
=（5，4）-（2，3）=（3，1），
=（7，10）-（2，3）=（5，7），
=（a，a）-（2，3）=（a-2，a-3）．
∵
=
+λ•
(λ∈R)，
∴（a-2，a-3）=（3，1）+λ（5，7），
∴
，解得λ=
．
（2）设P（x，y），∴
=（x，y）-（2，3）=（x-2，y-3）．
∵
=
+λ•
(λ∈R)，
∴（x-2，y-3）=（3，1）+λ（5，7）=（3+5λ，1+7λ），
∴
，化为
，
∵点P在第三象限，∴
，
解得λ＜-1．
∴λ的取值范围是（-∞，-1）．
| AB |
| AC |
| AP |
∵
| AP |
| AB |
| AC |
∴（a-2，a-3）=（3，1）+λ（5，7），
∴
|
| 1 |
| 2 |
（2）设P（x，y），∴
| AP |
∵
| AP |
| AB |
| AC |
∴（x-2，y-3）=（3，1）+λ（5，7）=（3+5λ，1+7λ），
∴
|
|
∵点P在第三象限，∴
|
解得λ＜-1．
∴λ的取值范围是（-∞，-1）．
点评：本题考查了向量的线性运算、向量基本定理、点在象限的特点，属于基础题．
练习册系列答案
相关题目
复数z=
（i是虚数单位）在复平面内的对应点位于（ ）
| ||
1-
|
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
阅读如图所示程序框图，运行相应的程序，输出s的值等于（ ）
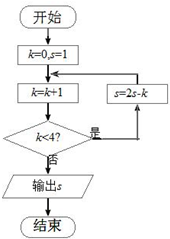
| A、-3 | B、-10 | C、0 | D、-2 |
如图，抛物线C的顶点为O（0，0），焦点在y轴上，抛物线上的点（x0，1）到焦点的距离为2．
