题目内容
19．已知矩阵M=$[\begin{array}{l}{1}&{a}\\{-1}&{b}\end{array}]$，点（1，-1）在M对应的变换作用下得到点（-1，5），求矩阵M的特征值．分析 设出矩阵，利用特征向量的定义，即二阶变换矩阵的概念，建立方程组，即可得到结论．
解答 解：由题意，$[\begin{array}{l}{1}&{a}\\{-1}&{b}\end{array}]$$[\begin{array}{l}{1}\\{-1}\end{array}]$=$[\begin{array}{l}{-1}\\{5}\end{array}]$，即$\left\{\begin{array}{l}{1-a=-1}\\{-1-b=-5}\end{array}\right.$，解得a=2，b=4，所以矩阵M=$[\begin{array}{l}{1}&{2}\\{-1}&{4}\end{array}]$．
所以矩阵M的特征多项式为f（λ）=$|\begin{array}{l}{λ-1}&{-2}\\{1}&{λ-4}\end{array}|$=λ2-5λ+6，令f（λ）=0，得矩阵M的特征值为2和3．
点评 本题考查特征值，考查二阶变换矩阵，考查学生的计算能力，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
2．已知直线x+y=m（m＞0）与圆x2+y2=1相交于P，Q两点，且∠POQ=120°（其中O为原点），那么m的值是（ ）
| A． | $\frac{{\sqrt{3}}}{3}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $\sqrt{2}$ | D． | $\sqrt{3}$ |
4．已知x，y∈R，（ ）
| A． | 若|x-y2|+|x2+y|≤1，则${（x+\frac{1}{2}）^2}+{（y-\frac{1}{2}）^2}≤\frac{3}{2}$ | |
| B． | 若|x-y2|+|x2-y|≤1，则${（x-\frac{1}{2}）^2}+{（y-\frac{1}{2}）^2}≤\frac{3}{2}$ | |
| C． | 若|x+y2|+|x2-y|≤1，则${（x+\frac{1}{2}）^2}+{（y+\frac{1}{2}）^2}≤\frac{3}{2}$ | |
| D． | 若|x+y2|+|x2+y|≤1，则${（x-\frac{1}{2}）^2}+{（y+\frac{1}{2}）^2}≤\frac{3}{2}$ |
8．
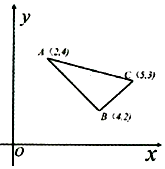已知点（x，y）在△ABC所包围的阴影区域内（包括边界），若有且仅有B（4，2）是使得z=ax-y取得最大值的最优解，则实数a的取值范围为（ ）
已知点（x，y）在△ABC所包围的阴影区域内（包括边界），若有且仅有B（4，2）是使得z=ax-y取得最大值的最优解，则实数a的取值范围为（ ）| A． | -1＜a＜1 | B． | -1≤a≤1 | C． | -1≤a＜1 | D． | -1＜a≤1 |