题目内容

若
π
4
＜α＜β＜
π
2
，sinα+cosα=a，sinβ+cosβ=b，则a，b的大小关系是
 
．
考点：两角和与差的正弦函数
专题：三角函数的求值
分析：化简可得a=
2
sin（α+
π
4
），b=
2
sin（β+
π
4
），又可得
π
2
＜α+
π
4
＜β+
π
4
＜
3π
4
，由正弦函数的单调性可得．
解答： 解：化简可得a=sinα+cosα=
2
sin（α+
π
4
），
b=sinβ+cosβ=
2
sin（β+
π
4
），
∵
π
4
＜α＜β＜
π
2
，∴
π
2
＜α+
π
4
＜β+
π
4
＜
3π
4
，
由正弦函数的单调性可知a＞b
故答案为：a＞b
点评：本题考查两角和与差的正弦函数，涉及三角函数的单调性，属基础题．
练习册系列答案
相关题目
在△ABC中，已知AC=1，∠BAC=60°，S△ABC=
3
．
（1）求sin∠ACB的值；
（2）记BC边上的中线为AD，求AD的长．
某化肥厂甲、乙两个车间负责包装肥料，在自动包装传送带上每隔30秒抽取一包产品，称其重量，分别记录抽查数据如下：
甲：102，111，89，98，103，98，99；
乙：104，111，87，100，99，98，101．
（1）这种抽样方法是那一种？
（2）将这两组数据用茎叶图表示；
（3）计算这两组数据的平均数和方差，说明那个车间的产品比较稳定．
△ABC的内角A，B，C的对边分别为a，b，c，已知b=3，三个内角A，B，C成等差数列．
（1）若cosC=
6
3
，求c；
（2）求
BA
•
BC
的最大值．
设a，b是正实数，以下不等式：（1）
a
b
+
b
a
＞2；（2）
2(a2+b2)
≥a+b；（3）
ab
≥
2ab
a+b
；（4）a＜|a-b|+b，其中恒成立的有（　　）
A、（1）（2）
B、（2）（3）
C、（3）（4）
D、（2）（4）
y=sin（2x-
π
3
）-sin2x的一个单调递增区间是（　　）
A、[-
π
6
，
π
3
]
B、[
π
12
，
7
12
π]
C、[
5
12
π，
13
12
π]
D、[
π
3
，
5π
6
]
已知空间四点A（4，1，3），B（2，3，1），C（3，7，-5），D（x，-1，3）共面，则x=（　　）
A、4B、1C、10D、11
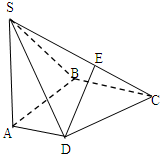四棱锥S-ABCD中，底面ABCD为直角梯形，AB垂直于AD和BC，SA⊥面ABCD，SA=AB=BC=2，AD=1．求：
（1）VS-ABCD；
（2）SC上是否存在点E，使DE⊥SB？若存在，确定点E的位置．
已知2x+3y+4z=1，则x2+y2+z2的最小值是  （　　）
A、
1
9
B、
1
13
C、
1
21
D、
1
29

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网