题目内容
奇函数f（x）在x＞0时，f（x）=x2-2x-3，则x＜0时f（x）=（ ）
| A、x2-2x+3 |
| B、x2+2x-3 |
| C、-x2-2x+3 |
| D、-x2-2x-3 |
考点：函数奇偶性的性质
专题：计算题,函数的性质及应用
分析：令x＜0，则-x＞0，由条件则有f（-x）=x2+2x-3，再由奇函数的定义，即可得到所求解析式．
解答：
解：令x＜0，则-x＞0，
在x＞0时，f（x）=x2-2x-3，
则有f（-x）=x2+2x-3，
又f（-x）=-f（x），
则f（x）=-x2-2x+3（x＜0），
故选C．
在x＞0时，f（x）=x2-2x-3，
则有f（-x）=x2+2x-3，
又f（-x）=-f（x），
则f（x）=-x2-2x+3（x＜0），
故选C．
点评：本题考查函数的奇偶性的运用：求解析式，考查运算能力，属于基础题．
练习册系列答案
相关题目
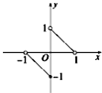定义在[-1，0）∪（0，1]的奇函数f（x），在（0，1]的图象如图，f（x）-f（-x）＞-1的解集是（ ）A、(-1，-
| ||
B、[-1，
| ||
C、(-
| ||
D、(-
|
在△ABC中，内角A，B，C的对边分别为a，b，c．若（a+b）（a-b）=c（b+c），则A=（ ）
| A、30° | B、60° |
| C、120° | D、150° |
设f（x）是R上的偶函数，且在（-∞，0）上为减函数，若x1＜0，x1+x2＞0，则（ ）
| A、f（x1）＞f（x2） |
| B、f（x1）=f（x2） |
| C、f（x1）＜f（x2） |
| D、不能确定f（x1）与f（x2）的大小 |