题目内容
12.已知函数y=sin2x+2sinxcosx+3cos2x,x∈R(1)求函数的最小正周期;
(2)求函数的单调增区间;
(3)求x取何时,函数取得最大值为多少.
分析 (1)利用三角函数的倍角公式进行化简,结合三角函数的周期公式即可求函数的最小正周期;
(2)结合三角函数的单调性即可求函数的单调增区间;
(3)利用三角函数的有界性即可求出函数的最大值.
解答 解:将y=sin2x+2sinxcosx+3cos2x,x∈R,整理得$y=sin2x+cos2x+2=\sqrt{2}sin(2x+\frac{π}{4})+2$.
(1)函数的最小正周期$T=\frac{2π}{2}=π$;
(2)由函数为增函数,则由$2kπ-\frac{π}{2}≤2x+\frac{π}{4}≤2kπ+\frac{π}{2}$,k∈Z.得$kπ-\frac{3π}{8}≤x≤kπ+\frac{π}{8}$,k∈Z.
那么函数的单调递增区间是$[kπ-\frac{3π}{8},kπ+\frac{π}{8}]$,k∈Z.
(3)$令2x+\frac{π}{4}=2kπ+\frac{π}{2},解得x=kπ+\frac{π}{8},k∈Z$,
此时函数取到最大值为$\sqrt{2}+2$.
点评 本题主要考查三角函数的图象和性质,利用三角函数的倍角公式进行化简是解决本题的关键.

练习册系列答案
相关题目
2.一个三棱锥的三视图如图所示,则它的体积为( )
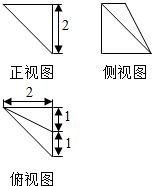

| A. | $\frac{2}{3}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | 2 |
17.三个数a=0.36,b=60.7,c=log0.5$\frac{3}{2}$的大小关系为( )
| A. | a>b>c | B. | a>c>b | C. | b>a>c | D. | c>a>b |