题目内容
设双曲线
-
=1(a>0,b>0)的渐近线与抛物线y=x2+1相切,则该双曲线的离心率等于( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
C、
| ||
| D、2 |
考点:双曲线的简单性质
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:求出双曲线的渐近线方程,代入抛物线方程,运用相切的条件:判别式为0,解方程,可得a,b的关系,再由双曲线的a,b,c的关系和离心率公式,计算即可得到.
解答:
解:双曲线
-
=1(a>0,b>0)的渐近线方程为y=±
x,
代入抛物线方程y=x2+1,
得x2±
x+1=0,
由相切的条件可得,判别式
-4=0,
即有b=2a,则c=
=
=
a,
则有e=
=
.
故选C.
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
代入抛物线方程y=x2+1,
得x2±
| b |
| a |
由相切的条件可得,判别式
| b2 |
| a2 |
即有b=2a,则c=
| a2+b2 |
| 4a2+a2 |
| 5 |
则有e=
| c |
| a |
| 5 |
故选C.
点评:本题考查双曲线的方程和性质,考查离心率的求法,考查直线和曲线相切的条件,考查运算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设集合A={x|y=lg(x-1)},B={y|y=2x,x∈R},则A∪B=( )
| A、∅ | B、R |
| C、(1,+∞) | D、(0,+∞) |
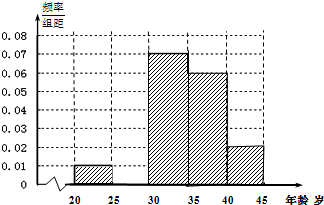 某市要对两千多名出租车司机的年龄进行调查,现从中随机抽出100名司机,已知抽到的司机年龄都在[20,45)岁之间,根据调查结果得出司机的年龄情况残缺的频率分布直方图如图所示,利用这个残缺的频率分布直方图估计该市出租车司机年龄的中位数大约是
某市要对两千多名出租车司机的年龄进行调查,现从中随机抽出100名司机,已知抽到的司机年龄都在[20,45)岁之间,根据调查结果得出司机的年龄情况残缺的频率分布直方图如图所示,利用这个残缺的频率分布直方图估计该市出租车司机年龄的中位数大约是