题目内容
已知平面内有一条线段AB,|AB|=4,动点P满足|PA|-|PB|=3,O为AB的中点,则|OP|的最小值为 .
考点:两点间距离公式的应用
专题:圆锥曲线的定义、性质与方程
分析:动点P满足|PA|-|PB|=3<4=|AB|,可得点P在双曲线
-
=1的右支上.即可得出.
| 4x2 |
| 9 |
| 4y2 |
| 7 |
解答:
解:∵动点P满足|PA|-|PB|=3<4=|AB|,
∴点P在双曲线
-
=1的右支上.
∴|OP|的最小值为a=
.
故答案为:
.
∴点P在双曲线
| 4x2 |
| 9 |
| 4y2 |
| 7 |
∴|OP|的最小值为a=
| 3 |
| 2 |
故答案为:
| 3 |
| 2 |
点评:本题考查了双曲线的定义及其性质,属于基础题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
如图,下列四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥平面MNP的图形序号是( )


| A、①② | B、③④ | C、②③ | D、①④ |
数列{an}的通项为an=(-1)n•n•sin
+1前n项和为Sn,S100=( )
| nπ |
| 2 |
| A、50 | B、100 |
| C、-150 | D、150 |
直线y=kx-2与椭圆x2+4y2=80相交于不同的两点P、Q,若PQ的中点横坐标为2,则直线的斜率等于( )
A、
| ||
B、
| ||
| C、2 | ||
| D、4 |
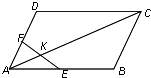 如图,一直线EF与平行四边形ABCD的两边AB,AD分别交于E、F两点,且交其对角线于K,其中,
如图,一直线EF与平行四边形ABCD的两边AB,AD分别交于E、F两点,且交其对角线于K,其中,