题目内容
设函数f（x）=3x+3-x，g（x）=3x-3-x的定义域均为R，则（ ）
| A、f（x）与g（x），均为奇函数 |
| B、f（x）与g（x）均为偶函数 |
| C、f（x）为奇函数，g（x）为偶函数 |
| D、f（x）为偶函数，g（x）为奇函数 |
考点：函数奇偶性的判断,函数的定义域及其求法
专题：函数的性质及应用
分析：本题直接根据函数的奇偶性，判断出函数f（x）、g（x）的奇偶性，得到本题结论．
解答：
解：∵定义在R上的函数f（x）=3x+3-x，
∴f（-x）=3-x+3x=f（x），
∴f（x）偶函数；
∵定义在R上的函数g（x）=3x-3-x
∴g（-x）=3-x-3x=-g（x），
∴g（x）是奇函数．
故选D．
∴f（-x）=3-x+3x=f（x），
∴f（x）偶函数；
∵定义在R上的函数g（x）=3x-3-x
∴g（-x）=3-x-3x=-g（x），
∴g（x）是奇函数．
故选D．
点评：本题考查了奇偶性，本题难度不大，属于基础题．
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
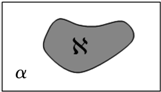假定平面内的一条直线将该平面内的一个区域分成面积相等的两个区域，则称这条直线平分这个区域．如图，?是平面α内的任意一个封闭区域．现给出如下结论：