题目内容
19.某化工厂产生的废气经过过滤后排放,以模型$y={P_0}{e^{-kx}}$去拟合过滤过程中废气的污染物数量ymg/L与时间xh间的一组数据时,为了求出回归方程,设z=lny,其变换后得到线性回归方程z=-0.5x+2+ln300,则当经过6h后,预报废气的污染物数量为( )| A. | 300e2mg/L | B. | 300emg/L | C. | $\frac{300}{e^2}$mg/L | D. | $\frac{300}{e}$mg/L |
分析 将x=6代入回归方程求出z,再将z代入z=lny得出y.
解答 解:当x=6时,z=-1+ln300=ln$\frac{300}{e}$,
∴y=ez=$\frac{300}{e}$.
故选:D.
点评 本题考查了回归方程的拟合估计,属于基础题.

练习册系列答案
相关题目
9.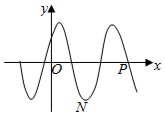 已知函数$f(x)=Acos(wx+φ)(w>0,|φ|<\frac{π}{2})$的部分图象如图所示,其中N,P的坐标分别为$(\frac{5}{8}π,-A),(\frac{11}{8}π,-0)$,则函数f(x)的单调递减区间不可能为( )
已知函数$f(x)=Acos(wx+φ)(w>0,|φ|<\frac{π}{2})$的部分图象如图所示,其中N,P的坐标分别为$(\frac{5}{8}π,-A),(\frac{11}{8}π,-0)$,则函数f(x)的单调递减区间不可能为( )
 已知函数$f(x)=Acos(wx+φ)(w>0,|φ|<\frac{π}{2})$的部分图象如图所示,其中N,P的坐标分别为$(\frac{5}{8}π,-A),(\frac{11}{8}π,-0)$,则函数f(x)的单调递减区间不可能为( )
已知函数$f(x)=Acos(wx+φ)(w>0,|φ|<\frac{π}{2})$的部分图象如图所示,其中N,P的坐标分别为$(\frac{5}{8}π,-A),(\frac{11}{8}π,-0)$,则函数f(x)的单调递减区间不可能为( )| A. | $[\frac{π}{8},\frac{5π}{8}]$ | B. | $[-\frac{7π}{8},-\frac{3π}{8}]$ | C. | $[\frac{9π}{4},\frac{21π}{8}]$ | D. | $[\frac{9π}{8},\frac{33π}{8}]$ |
4.利用计算机产生120个随机正整数,其最高位数字(如:34的最高位数字为3,567的最高位数字为5)的频数分布图如图所示,若从这120个正整数中任意取出一个,设其最高位数字为d(d=1,2,…,9)的概率为P,下列选项中,最能反映P与d的关系的是( )
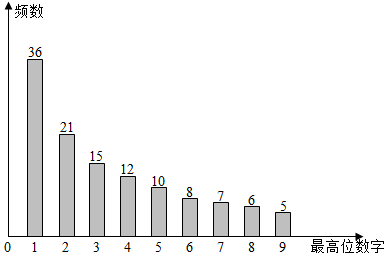

| A. | P=lg(1+$\frac{1}{d}$) | B. | P=$\frac{1}{d+2}$ | C. | P=$\frac{{(d-5)}^{2}}{120}$ | D. | P=$\frac{3}{5}$×$\frac{1}{{2}^{d}}$ |
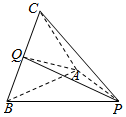 如图,在三棱锥P-ABC中,PA=PB=AB=BC=2,∠CBA=∠PBC=60°,Q为线段BC的中点.
如图,在三棱锥P-ABC中,PA=PB=AB=BC=2,∠CBA=∠PBC=60°,Q为线段BC的中点.