设实数x.y满足条件$\left\{\begin{array}{l}3x-y-2≤0\\ 2x-y≥0\\ y≥0\end{array}\right.$则目标函数z=2x+y的最大值为8．题目和参考答案——青夏教育精英家教网——

题目内容

16．设实数x，y满足条件$\left\{\begin{array}{l}3x-y-2≤0\\ 2x-y≥0\\ y≥0\end{array}\right.$则目标函数z=2x+y的最大值为8．

分析作出可行域，根据可行域判断目标函数的最优解位置．

解答解：作出约束条件表示的可行域如图所示：

由z=2x+y得y=-2x+z，
由可行域可知当直线y=-2x+z经过点B时，直线的截距最大，即z最大．
解方程组$\left\{\begin{array}{l}{2x-y=0}\\{3x-y-2=0}\end{array}\right.$得B（2，4）．
∴z的最大值为2×2+4=8．
故答案为：8．

点评本题考查了简单的线性规划，作出可行域判断最优解的位置是关键，属于中档题．

练习册系列答案

深圳市初中学业水平考试系列答案

小升初集结号系列答案

名著导读全析精练系列答案

学科教学基本要求系列答案

寒假学习与应用系列答案

活动填图册系列答案

有效课堂精讲精练系列答案

新课程初中物理同步训练系列答案

单元测评四川教育出版社系列答案

相关题目

6．已知函数f（x）=|x-1|-2|x+a|，a＞0
（1）若a=1时，求不等式f（x）＞1的解集；
（2）若f（x）的图象与x轴围成的三角形面积小于6，求a的取值范围．

7．已知等差数列{a_n}的通项公式${a_n}=3n-1（n∈{N^*}）$．设数列{b_n}为等比数列，且${b_n}={a_{k_n}}$．
（Ⅰ）若b₁=a₁=2，且等比数列{b_n}的公比最小，
（ⅰ）写出数列{b_n}的前4项；
（ⅱ）求数列{k_n}的通项公式；
（Ⅱ）证明：以b₁=a₂=5为首项的无穷等比数列{b_n}有无数多个．

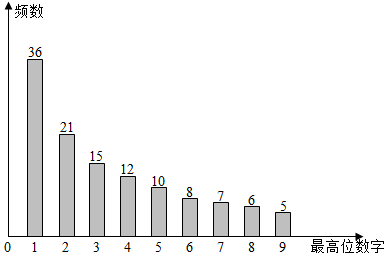
4．利用计算机产生120个随机正整数，其最高位数字（如：34的最高位数字为3，567的最高位数字为5）的频数分布图如图所示，若从这120个正整数中任意取出一个，设其最高位数字为d（d=1，2，…，9）的概率为P，下列选项中，最能反映P与d的关系的是（　　）

P=lg（1+$\frac{1}{d}$）

P=$\frac{1}{d+2}$

P=$\frac{{（d-5）}^{2}}{120}$

P=$\frac{3}{5}$×$\frac{1}{{2}^{d}}$

11．若有点M₁（4，3）和M₂（2，-1），点M分有向线段$\overrightarrow{{{M}_{1}M}_{2}}$的比λ=-2．则点M的坐标（0，-5）．

1．设向量$\overrightarrow{a}$=（4cosα，sinα），$\overrightarrow{b}$=（sinβ，4cosβ），$\overrightarrow{c}$=（cosβ，-4sinβ）
（]）若$\overrightarrow{a}$与$\overrightarrow{b}$-2$\overrightarrow{c}$垂直，求tan（α+β）的值；
（2）求|$\overrightarrow{b}$+$\overrightarrow{c}$|的最大值；
（3）若tanαtanβ=16，求证：$\overrightarrow{a}$∥$\overrightarrow{b}$．

8．已知f（x）满足下列条件，分别求f（x）的解析式．
（1）已知f（$\sqrt{x}$-1）=x-2$\sqrt{x}$，求f（x）；
（2）已知f（x）为二次函数，f（0）=0，f（x+1）=f（x）+x+1，求f（x）；
（3）已知f（x）满足f（x）+2f（-x）=$\frac{1}{1+x}$，求f（x）；
（4）已知f（x）为偶函数，且对于任意实数x，y，都有f（x+y）=f（x）+f（y）+xy，求f（x）的解析式．

5．n∈N^*，A${\;}_{n}^{3}$+A${\;}_{4}^{n+1}$的值为30．

6．已知关于x的不等式（ax一1）（x十1）＜0的解集为（-∞，-1）∪（-$\frac{1}{2}$，+∞），求a的值．