题目内容
在△ABC中,角A,B,C的对边分别为a,b,c,AH为BC边上的高,给出以下四个结论:
①
•
=0;
②
•(
+
)=
•
;
③若
•
>0,则△ABC为锐角三角形;
④
•
=csinB.
其中所有正确结论的序号是 .
①
| AH |
| BC |
②
| AH |
| AB |
| BC |
| AH |
| AB |
③若
| AB |
| AC |
④
| AC |
| ||
|
|
其中所有正确结论的序号是
考点:命题的真假判断与应用
专题:平面向量及应用
分析:△ABC中,由AH为BC边上的高,得出
⊥
,判定①正确;
由
+
=
,得出
•(
+
)=
•
=|
|2,
•
=|
|2,判定②正确;
由
•
>0,得出角A是锐角,不能得出角B、C都是锐角,判定③错误;
由
•
=
=|
|=csinB,判定④正确.
| AH |
| BC |
由
| AB |
| BC |
| AC |
| AH |
| AB |
| BC |
| AH |
| AC |
| AH |
| AH |
| AB |
| AH |
由
| AB |
| AC |
由
| AC |
| ||
|
|
| ||||
|
|
| AH |
解答:
解:对于①,△ABC中,∵AH为BC边上的高,∴
⊥
,∴
•
=0,∴①正确;
对于②,如图,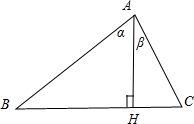 ;
;
△ABC中,
+
=
,∴
•(
+
)=
•
=|
|×|
|×cosβ=|
|×|
|×
=|
|2,
同理,
•
=|
|2,∴
•(
+
)=
•
;∴②正确;
对于③,∵
•
>0,∴角A是锐角,不能说明角B、C是锐角,∴③错误;
对于④,
•
=
=
=|
|=AB•sinB=csinB,∴④正确;
综上,正确的结论是①②④.
故答案为:①②④.
| AH |
| BC |
| AH |
| BC |
对于②,如图,
 ;
;△ABC中,
| AB |
| BC |
| AC |
| AH |
| AB |
| BC |
| AH |
| AC |
| AH |
| AC |
| AH |
| AC |
|
| ||
|
|
| AH |
同理,
| AH |
| AB |
| AH |
| AH |
| AB |
| BC |
| AH |
| AB |
对于③,∵
| AB |
| AC |
对于④,
| AC |
| ||
|
|
| ||||
|
|
|
| ||
|
|
| AH |
综上,正确的结论是①②④.
故答案为:①②④.
点评:本题通过命题真假的判定,考查了平面向量的综合应用问题,解题时应画出图形,结合图形,对每一个选项进行分析,从而作出正确的选择,是易错题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
从集合A={1,2,3,4,5}任意取出两个数,这两个数的和是偶数的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设随机变量ξ~N(3,σ2),若P(ξ≥7)=0.16,则P(-1≤ξ≤7)=( )
| A、0.84 | B、0.68 |
| C、0.32 | D、0.16 |
从数字0,1,2,3,…,9中,按由小到大的顺序取出a1,a2,a3,且a2-a1≥2,a3-a2≥2,则不同的取法有( )
| A、20种 | B、35种 |
| C、56种 | D、60种 |
若不等式a+2b+3>(
+2
)λ对任意正数a,b恒成立,则实数λ的取值范围为( )
| a |
| b |
| A、(-∞,3) | ||
| B、(-∞,2) | ||
| C、(-∞,1) | ||
D、(-∞,
|