题目内容
若不等式a+2b+3＞（
+2
）λ对任意正数a，b恒成立，则实数λ的取值范围为（ ）
| a |
| b |
| A、（-∞，3） | ||
| B、（-∞，2） | ||
| C、（-∞，1） | ||
D、（-∞，
|
考点：基本不等式
专题：不等式的解法及应用
分析：将不等式化为λ＜
，由基本不等式求
的最小值即可．
| a+2b+3 | ||||
|
| a+2b+3 | ||||
|
解答：
解：不等式a+2b+3＞（
+2
）λ
可化为λ＜
，
∵a+2b+3=（a+1）+2（b+1）
≥2
+2×2
=2（
+2
），
∴当a=b=1时，
取最小值2，
∴λ＜2
故选：B
| a |
| b |
可化为λ＜
| a+2b+3 | ||||
|
∵a+2b+3=（a+1）+2（b+1）
≥2
| a |
| b |
| a |
| b |
∴当a=b=1时，
| a+2b+3 | ||||
|
∴λ＜2
故选：B
点评：本题考查不等式的性质，基本不等式的应用，属基础题．
练习册系列答案
中考解读考点精练系列答案
各地期末复习特训卷系列答案
相关题目
已知△ABC中，|
|=2，A=
，则|
+
|有（ ）
| BC |
| π |
| 3 |
| AB |
| AC |
A、最大值
| ||
B、最大值2
| ||
C、最小值
| ||
D、最小值2
|
已知i为复数单位，若
=1+bi（a，b∈R），则a+b=（ ）
| 1+ai |
| i |
| A、2 | B、1 | C、-1 | D、0 |
对于命题p：若|
|=|
|=2，
与
的夹角是
，则向量
在
方向上的投影是1；命题q：“x≤1”是“
≥1”的必要不充分条件，下列判断正确的是（ ）
| a |
| b |
| a |
| b |
| 2π |
| 3 |
| b |
| a |
| 1 |
| x |
| A、￢q为假命题 |
| B、￢p为假命题 |
| C、“p∧q”是真命题 |
| D、“p∨q”是假命题 |
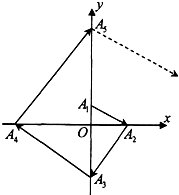如图所示，点列{An}满足：|| OA1 |
| OAi+1 |
| OAi |
| OA1 |
| OA2 |
| OA2014 |
| A、（22014-1，0） | ||||
| B、（22016-1，22015-1） | ||||
C、（
| ||||
D、（
|
已知函数f（x）=loga（2x+b-1）（a＞0且a≠1）的部分图象如图所示，则满足a，b关系是（ ）
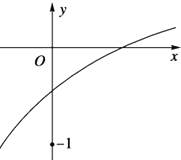
A、0＜
| ||||
B、0＜b＜
| ||||
C、0＜
| ||||
D、0＜
|