题目内容

2．已知下面四个命题：
（1）从匀速传递的产品生产流水线上，质检员每15分钟从中抽取一件产品进行某项指标检测，这样的抽样是系统抽样；
（2）两个随机变量相关性越强，则相关系数的绝对值越接近于1；
（3）对分类变量X和Y的随机变量K2的观测值k来说，k越小，“X与Y有关系”的把握程度越大；
（4）在回归直线方程$\widehat{y}$=0.4x+12中，当解释变量x每增加一个单位时，预报变量大约增加0.4个单位．
其中所有真命题的序号是（1）（2）（4）．

分析 根据系统抽样的定义，可判断（1）；根据相关系数的几何意义，可判断（2）；根据观测值的意义，可判断（3）；根据回归系数的几何意义，可判断（4）．

解答 解：（1）从匀速传递的产品生产流水线上，质检员每15分钟从中抽取一件产品进行某项指标检测，
这样的抽样是等间隔的，是系统抽样，故（1）正确；
（2）两个随机变量相关性越强，则相关系数的绝对值越接近于1，故（2）正确；
（3）对分类变量X和Y的随机变量K2的观测值k来说，k越小，“X与Y有关系”的把握程度越小，故（3）错误；
（4）在回归直线方程$\widehat{y}$=0.4x+12中，当解释变量x每增加一个单位时，预报变量大约增加0.4个单位，故（4）正确．
故答案为：（1）（2）（4）

点评 本题以命题的真假判断与应用为载体，考查了抽样方法，相关系数，独立性检验，回归分析，难度基础．

练习册系列答案
相关题目
14．过抛物线y2=2px（p＞0）的焦点F作倾斜角为60°的直线l，若直线l与抛物线在第一象限的交点为A并且点A也在双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一条渐近线上，则双曲线的离心率为$\frac{{\sqrt{21}}}{3}$．
13．已知定义域为R的奇函数f（x）的导函数为f′（x），当x≠0时，f′（x）+$\frac{f（x）}{x}$＞0，若a=$\frac{1}{2}$f（$\frac{1}{2}$），b=-2f（-2），c=ln$\frac{1}{2}$f（-ln 2），则下列关于a，b，c的大小关系正确的是（　　）
A．a＞b＞cB．a＜c＜bC．c＞b＞aD．b＞a＞c
10．已知函数f（x）=$\left\{\begin{array}{l}{2^x}-1，x＞0\\-{x^2}-2x，x≤0\end{array}\right.$
（1）求f（1）的值；
（2）画出函数f（x）的图象并写出该函数的单调区间．
17．一次测试中，为了了解学生的学习情况，从中抽取了n个学生的成绩进行统计．按照的分组作出频率分布直方图，并作出样本分数的茎叶图（图中仅列出得分在的数据）．

（1）求样本容量n和频率分布直方图中x，y的值；
（2）求这n名同学成绩的平均数、中位数及众数；
（3）在选取的样本中，从成绩是80分以上（含80分）的同学中随机抽取3名参加志愿者活动，所抽取的3名同学中至少有一名成绩在[90，100]内的概率．
7．已知m、n、s、t∈R*，m+n=3，$\frac{m}{s}+\frac{n}{t}=1$其中m、n是常数且m＜n，若s+t的最小值 是$3+2\sqrt{2}$，满足条件的点（m，n）是椭圆$\frac{x^2}{4}+\frac{y^2}{16}=1$一弦的中点，则此弦所在的直线方程为（　　）
A．x-2y+3=0B．4x-2y-3=0C．x+y-3=0D．2x+y-4=0
14．命题p：2017是奇数，q：2016是偶数，则下列说法中正确的是（　　）
A．p或q为真B．p且q为假C．非p为真D．非q为真
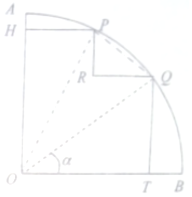11．现有一圆心角为$\frac{π}{2}$，半径为12cm的扇形铁皮（如图）．P，Q是弧AB上的动点且劣弧$\widehat{PQ}$的长为2πcm，过P，Q分别作与OA，OB平行或垂直的线，从扇形上裁剪出多边形OHPRQT，将该多边形面积表示为角α的函数，并求出其最大面积是多少？
12．已知函数f（x）=$\left\{\begin{array}{l}{{2}^{-x}，x≤0}\\{-lnx，x＞0}\end{array}\right.$若关于x的方程f2（x）+f（x）+m=0有三个不同实数根，则m的取值范围是（　　）
A．$m＜\frac{1}{4}$B．m≤-2C．$-2≤m＜\frac{1}{4}$D．m＞2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网