题目内容
11.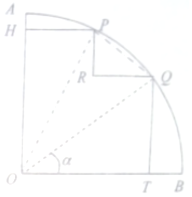 现有一圆心角为$\frac{π}{2}$,半径为12cm的扇形铁皮(如图).P,Q是弧AB上的动点且劣弧$\widehat{PQ}$的长为2πcm,过P,Q分别作与OA,OB平行或垂直的线,从扇形上裁剪出多边形OHPRQT,将该多边形面积表示为角α的函数,并求出其最大面积是多少?
现有一圆心角为$\frac{π}{2}$,半径为12cm的扇形铁皮(如图).P,Q是弧AB上的动点且劣弧$\widehat{PQ}$的长为2πcm,过P,Q分别作与OA,OB平行或垂直的线,从扇形上裁剪出多边形OHPRQT,将该多边形面积表示为角α的函数,并求出其最大面积是多少?
分析 连接OQ,OP,则∠POQ=$\frac{π}{6}$,求出面积,利用三角函数知识求最值,即可得出结论.
解答 解:连接OQ,OP,则∠POQ=$\frac{π}{6}$.
设∠QOB=α,多边形OHPRQT的面积为S,则∠POB=α+$\frac{π}{6}$,α∈(0,$\frac{π}{3}$),
S=12sinα•12cosα+12sin(α+$\frac{π}{6}$)•12cos(α+$\frac{π}{6}$)-12sinα•12cos(α+$\frac{π}{6}$)=(72$\sqrt{3}$-72)sin(2α+$\frac{π}{6}$)+36,
α=$\frac{π}{6}$,即∠POA=∠QOB=$\frac{π}{6}$时,多边形OHPRQT的面积的最大值为72$\sqrt{3}$-36(cm2).
点评 本题考查的知识点是在实际问题中建立三角函数模型,三角函数降幂公式及三角函数的最值,

练习册系列答案
相关题目
16.已知命题p:|x-4|≤6,q:x2-m2-2x+1≤0(m>0),若¬p是¬q的必要不充分条件,则实数m的取值范围为( )
| A. | [9,13] | B. | (3,9) | C. | [9,+∞) | D. | (9,+∞) |
20.若函数f(x)=aex-x-2a有两个零点,则实数a的取值范围是( )
| A. | $({-∞,\frac{1}{e}})$ | B. | $({0,\frac{1}{e}})$ | C. | (-∞,0) | D. | (0,+∞) |
1.向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,$\overrightarrow{a}$•($\overrightarrow{a}$+$\overrightarrow{b}$)=0,则$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影为( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | 0 | D. | $-\frac{{\sqrt{3}}}{2}$ |