题目内容
14.过抛物线y2=2px(p>0)的焦点F作倾斜角为60°的直线l,若直线l与抛物线在第一象限的交点为A并且点A也在双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线上,则双曲线的离心率为$\frac{{\sqrt{21}}}{3}$.分析 由题意画出图形,把A的坐标用p表示,代入双曲线的渐近线方程得到a,b的关系,结合a2+b2=c2求得双曲线的离心率.
解答 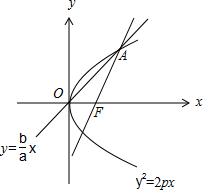 解:如图,设A(x0,y0),则|AF|=2(x0-$\frac{p}{2}$),
解:如图,设A(x0,y0),则|AF|=2(x0-$\frac{p}{2}$),
又|AF|=x0+$\frac{p}{2}$,∴2(x0-$\frac{p}{2}$)=x0+$\frac{p}{2}$
解得x0=$\frac{3p}{2}$,y0=$\frac{\sqrt{3}}{2}$|AF|=$\sqrt{3}$p,
∵点A在双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线上,
∴$\sqrt{3}$p=$\frac{b}{a}•\frac{3}{2}p$,解得:${b}^{2}=\frac{4}{3}{a}^{2}$,
由a2+b2=c2,得$\frac{{c}^{2}}{{a}^{2}}$=$\frac{7}{3}$,∴e=$\frac{{\sqrt{21}}}{3}$.
故答案为$\frac{{\sqrt{21}}}{3}$.:
点评 本题考查了抛物线与双曲线的几何性质,考查了数形结合的解题思想方法和数学转化思想方法,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
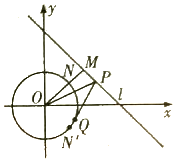 已知圆O:x2+y2=2,直线l过点$M(\frac{3}{2},\frac{3}{2})$,且OM⊥l,P(x0,y0)是直线l上的动点,线段OM与圆O的交点为点N,N'是N关于x轴的对称点.
已知圆O:x2+y2=2,直线l过点$M(\frac{3}{2},\frac{3}{2})$,且OM⊥l,P(x0,y0)是直线l上的动点,线段OM与圆O的交点为点N,N'是N关于x轴的对称点.