题目内容
13.已知定义域为R的奇函数f(x)的导函数为f′(x),当x≠0时,f′(x)+$\frac{f(x)}{x}$>0,若a=$\frac{1}{2}$f($\frac{1}{2}$),b=-2f(-2),c=ln$\frac{1}{2}$f(-ln 2),则下列关于a,b,c的大小关系正确的是( )| A. | a>b>c | B. | a<c<b | C. | c>b>a | D. | b>a>c |
分析 构造函数g(x)=xf(x),根据条件讨论g(x)的奇偶性和单调性,利用g(x)的单调性比较大小.
解答 解:设g(x)=xf(x),则g’(x)=f(x)+xf‘(x),
∵f′(x)+$\frac{f(x)}{x}$=$\frac{f(x)+xf′(x)}{x}$=$\frac{g′(x)}{x}$>0,
∴当x<0时,g′(x)<0,当x>0时,g′(x)>0,
∴g(x)在(-∞,0)上是减函数,在(0,+∞)上是增函数,
∵f(x)是定义在R上的奇函数,∴g(x)是R上的偶函数,
∵a=g($\frac{1}{2}$),b=g(-2)=g(2),c=ln$\frac{1}{2}$f(-ln2)=-ln2f(-ln2)=g(-ln2)=g(ln2),且$\frac{1}{2}<$ln2<2,
∴g($\frac{1}{2}$)<g(ln2)<g(2),即a<c<b
故选B.
点评 本题考查了函数单调性的判断和应用,属于中档题.

练习册系列答案
相关题目
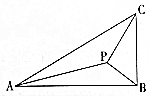 如图,在Rt△ABC中,两条直角边分别为AB=2$\sqrt{3}$,BC=2,P为△ABC内一点,∠BPC=90°,若∠APB=150°,则tan∠PBA=$\frac{\sqrt{3}}{4}$.
如图,在Rt△ABC中,两条直角边分别为AB=2$\sqrt{3}$,BC=2,P为△ABC内一点,∠BPC=90°,若∠APB=150°,则tan∠PBA=$\frac{\sqrt{3}}{4}$.