题目内容
17.一次测试中,为了了解学生的学习情况,从中抽取了n个学生的成绩进行统计.按照的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出得分在的数据).
(1)求样本容量n和频率分布直方图中x,y的值;
(2)求这n名同学成绩的平均数、中位数及众数;
(3)在选取的样本中,从成绩是80分以上(含80分)的同学中随机抽取3名参加志愿者活动,所抽取的3名同学中至少有一名成绩在[90,100]内的概率.
分析 (1)根据频率分布直方图的性质求得样本容量n和频率分布直方图中x、y的值;
(2)根据频率分布直方图分别求出这40名同学成绩的平均数、中位数及众数即可;
(3)由题意可知,分数在[80,90)内的有4人,分数在[90,100]内的有2人,根据条件概率求出即可.
解答 解:(1)由题意可知,
样本容量n=$\frac{8}{0.02×10}$=40,
y=$\frac{2}{40}$÷10=0.005,
x=$\frac{1-(0.02+0.04+0.01+0.005)×10}{10}$=0.025.
(2)由频率分布直方图得:
[50,60)有0.2×40=8人,
[60,70)有0.25×40=10人,
[70,80)有0.4×40=16人,
[80,9)有0.1×40=4人,
[90,100]有0.05×40=2人,
故平均数是:$\frac{8×55+10×65+16×75+4×85+2×95}{40}$=70.5;
中位数:71.25;众数:75;
(3)由题意,分数在[80,90)内的有4人,
分数在[90,100]内的有2人,
成绩是80分以上(含80分)的学生共6人.
P(X=2)=$\frac{{{C}_{4}^{2}C}_{2}^{1}}{{C}_{6}^{3}}$=$\frac{3}{5}$.
点评 本题主要考查等可能事件的概率,频率分布直方图的应用,属于中档题.

练习册系列答案
相关题目
5.在证明f(x)=2x+1为增函数的过程中,有下列四个命题:
①增函数的定义是大前提;
②增函数的定义是小前提;
③函数f(x)=2x+1满足增函数的定义是小前提;
④函数f(x)=2x+1满足增函数的定义是大前提;
其中正确的命题是( )
①增函数的定义是大前提;
②增函数的定义是小前提;
③函数f(x)=2x+1满足增函数的定义是小前提;
④函数f(x)=2x+1满足增函数的定义是大前提;
其中正确的命题是( )
| A. | ①② | B. | ②④ | C. | ①③ | D. | ② |
12.已知f(x)=tan(2x+$\frac{π}{4}$),则使f(x)≥$\sqrt{3}$成立的x的集合是( )
| A. | [$\frac{π}{24}$+$\frac{1}{2}$kπ,$\frac{π}{8}$+$\frac{1}{2}$kπ),k∈Z | B. | (-$\frac{π}{8}$+$\frac{1}{2}$kπ,$\frac{π}{24}$+$\frac{1}{2}$kπ),k∈Z | ||
| C. | [$\frac{π}{24}$+kπ,$\frac{π}{8}$+kπ),k∈Z | D. | [$\frac{π}{24}$+kπ,$\frac{π}{8}$+kπ],k∈Z |
7.若过点M(1,1)的直线l与圆(x-2)2+y2=4相较于两点A,B,且M为弦的中点AB,则|AB|为( )
| A. | $2\sqrt{2}$ | B. | 4 | C. | $\sqrt{2}$ | D. | 2 |
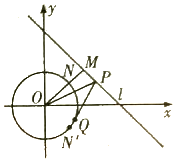 已知圆O:x2+y2=2,直线l过点$M(\frac{3}{2},\frac{3}{2})$,且OM⊥l,P(x0,y0)是直线l上的动点,线段OM与圆O的交点为点N,N'是N关于x轴的对称点.
已知圆O:x2+y2=2,直线l过点$M(\frac{3}{2},\frac{3}{2})$,且OM⊥l,P(x0,y0)是直线l上的动点,线段OM与圆O的交点为点N,N'是N关于x轴的对称点.