题目内容
设某种动物由出生算起活到20岁的概率为0.8,活到25岁的概率为0.4,现在一个20岁的这种动物,它能活到25岁的概率是 .
考点:条件概率与独立事件
专题:计算题,概率与统计
分析:根据事件间的保函关系,结合条件概率公式,可得结论.
解答:
解:设A=“能活到20岁”,B=“能活到25岁”,则P(A)=0.8,P(B)=0.4,
而所求概率为P(B|A),由于B⊆A,故A∩B=B,
于是P(B|A)=
=
=
=0.5,
所以这个动物能活到25岁的概率是0.5.
故答案为:0.5.
而所求概率为P(B|A),由于B⊆A,故A∩B=B,
于是P(B|A)=
| P(A∩B) |
| P(A) |
| P(B) |
| P(A) |
| 0.4 |
| 0.8 |
所以这个动物能活到25岁的概率是0.5.
故答案为:0.5.
点评:本题考点是条件概率,考查利用条件概率的公式建立方程求概率的能力,对于条件概率的问题,要弄清楚谁在谁的条件下发生,即要清楚了解事件之间的关系,再利用公式建立相关的方程正确求解.

练习册系列答案
相关题目
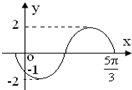 已知函数f(x)=2sin(ωx+φ)(ω>0,-π<φ<π)图象的一部分(如图所示),则ω与φ的值分别为( )
已知函数f(x)=2sin(ωx+φ)(ω>0,-π<φ<π)图象的一部分(如图所示),则ω与φ的值分别为( )A、
| ||||
B、1,-
| ||||
C、
| ||||
D、
|
 如图,△OAB是等腰三角形,P是底边AB延长线上一点,且PO=3,PA•PB=4,则腰长OA=
如图,△OAB是等腰三角形,P是底边AB延长线上一点,且PO=3,PA•PB=4,则腰长OA=
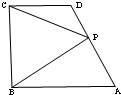 如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设