题目内容
11.已知函数$f(x)=3sin(ωx+\frac{π}{3})$的最小正周期为π,将函数f(x)的图象向右平移$\frac{π}{6}$个所得图象对应的函数为y=g(x),则关于函数为y=g(x)的性质,下列说法不正确的是( )| A. | g(x)为奇函数 | B. | 关于直线$x=\frac{π}{2}$对称 | ||
| C. | 关于点(π,0)对称 | D. | 在$(-\frac{π}{6},\frac{π}{4})$上递增 |
分析 由已知利用三角函数周期公式可求ω,利用函数y=Asin(ωx+φ)的图象变换可求g(x),利用正弦函数的图象和性质逐一判断各个选项即可得解.
解答 解:∵$f(x)=3sin(ωx+\frac{π}{3})$的最小正周期为π,
∴π=$\frac{2π}{ω}$,解得:ω=2,
∴f(x=3sin(2x+$\frac{π}{3}$),
∴将函数f(x)的图象向右平移$\frac{π}{6}$个所得图象对应的函数为y=g(x)=3sin[2(x-$\frac{π}{6}$)+$\frac{π}{3}$]=3sin2x,
对于A,g(-x)=3sin(-2x)=-3sin2x=-g(x),正确;
对于B,由于g($\frac{π}{2}$)=3sin(2×$\frac{π}{2}$)=0≠±3,故错误;
对于C,令2x=kπ,k∈Z,解得:x=$\frac{1}{2}$kπ,k∈Z,当k=2时,可得关于点(π,0)对称,正确;
对于D,令2kπ-$\frac{π}{2}$≤2x≤2kπ+$\frac{π}{2}$,k∈Z,解得:kπ-$\frac{π}{4}$≤x≤kπ+$\frac{π}{4}$,k∈Z,
可得,当k=0时,函数单调递增区间为:[-$\frac{π}{4}$,$\frac{π}{4}$],由于$(-\frac{π}{6},\frac{π}{4})$?[-$\frac{π}{4}$,$\frac{π}{4}$],故正确.
故选:B.
点评 本题主要考查了三角函数周期公式,函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象和性质,考查了转化思想,属于基础题.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
2.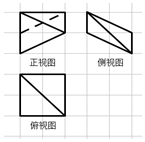 如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体的三视图,则该几何体的体积为( )
如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体的三视图,则该几何体的体积为( )
 如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体的三视图,则该几何体的体积为( )
如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体的三视图,则该几何体的体积为( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{8}{3}$ | D. | 4 |
1.2016年1月1日起全国统一实施全面的两孩政策.为了解适龄民众对放开生育二胎政策的态度,某市选取70后80后作为调查对象,随机调查了100人并对调查结果进行统计,70后不打算生二胎的占全部调查人数的15%,80后打算生二胎的占全部被调查人数的45%,100人中共有75人打算生二胎.
(1)根据调查数据,判断是否有90%以上把握认为“生二胎与年龄有关”,并说明理由;
(2)以这100人的样本数据估计该市的总体数据,且以频率估计概率,若从该市70后公民中(人数很多)随机抽取3位,记其中打算生二胎的人数为X,求随机变量X的分布列,数学期望E(X)和方差D(X).
参考公式:
(${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,其中n=a+b+c+d)
(1)根据调查数据,判断是否有90%以上把握认为“生二胎与年龄有关”,并说明理由;
(2)以这100人的样本数据估计该市的总体数据,且以频率估计概率,若从该市70后公民中(人数很多)随机抽取3位,记其中打算生二胎的人数为X,求随机变量X的分布列,数学期望E(X)和方差D(X).
参考公式:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
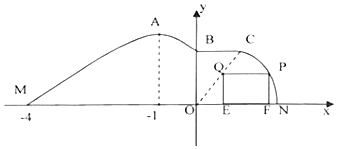 “中国齐云山国际养生万人徒步大会”得到了国内外户外运动爱好者的广泛关注,为了使基础设施更加完善,现需对部分区域进行改造.如图,在道路 北侧准备修建一段新步道,新步道开始部分的曲线段MAB是函数y=2sin(ωx+ϕ),(ω>0,0<ϕ<π),x∈[-4,0]的图象,且图象的最高点为A(-1,2).中间部分是长为1千米的直线段BC,且BC∥MN.新步道的最后一部分是以原点O为圆心的一段圆弧CN.
“中国齐云山国际养生万人徒步大会”得到了国内外户外运动爱好者的广泛关注,为了使基础设施更加完善,现需对部分区域进行改造.如图,在道路 北侧准备修建一段新步道,新步道开始部分的曲线段MAB是函数y=2sin(ωx+ϕ),(ω>0,0<ϕ<π),x∈[-4,0]的图象,且图象的最高点为A(-1,2).中间部分是长为1千米的直线段BC,且BC∥MN.新步道的最后一部分是以原点O为圆心的一段圆弧CN.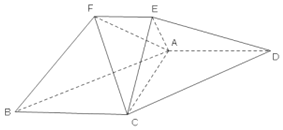 在如图所示的几何体中,平面ACE⊥平面ABCD,四边形ABCD 为平行四边形,
在如图所示的几何体中,平面ACE⊥平面ABCD,四边形ABCD 为平行四边形,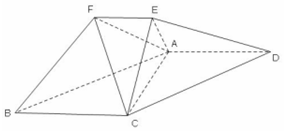 在如图所示的几何体中,平面ACE⊥平面ABCD,四边形ABCD 为平行四边形,
在如图所示的几何体中,平面ACE⊥平面ABCD,四边形ABCD 为平行四边形,