题目内容
20.若单位向量$\overrightarrow{e_1},\overrightarrow{e_2}$满足$|2\overrightarrow{e_1}+\overrightarrow{e_2}|=|\overrightarrow{e_1}|$,则$\overrightarrow{e_1}$在$\overrightarrow{e_2}$方向上投影为-1.分析 对$|2\overrightarrow{{e}_{1}}+\overrightarrow{{e}_{2}}|=|\overrightarrow{{e}_{1}}|$两边平方,并进行数量积的运算即可求出$cos<\overrightarrow{{e}_{1}},\overrightarrow{{e}_{2}}>$的值,从而可求出$\overrightarrow{{e}_{1}}$在$\overrightarrow{{e}_{2}}$方向上的投影.
解答 解:∵$|2\overrightarrow{{e}_{1}}+\overrightarrow{{e}_{2}}|=|\overrightarrow{{e}_{1}}|$;
∴$(2\overrightarrow{{e}_{1}}+\overrightarrow{{e}_{2}})^{2}={\overrightarrow{{e}_{1}}}^{2}$;
即$4{\overrightarrow{{e}_{1}}}^{2}+4\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}+{\overrightarrow{{e}_{2}}}^{2}={\overrightarrow{{e}_{1}}}^{2}$;
∴$4+4cos<\overrightarrow{{e}_{1}},\overrightarrow{{e}_{2}}>+1=1$;
∴$cos<\overrightarrow{{e}_{1}},\overrightarrow{{e}_{2}}>=-1$;
∴$\overrightarrow{{e}_{1}}$在$\overrightarrow{{e}_{2}}$方向上的投影为$|\overrightarrow{{e}_{1}}|cos<\overrightarrow{{e}_{1}},\overrightarrow{{e}_{2}}>=-1$.
故答案为:-1.
点评 考查单位向量的概念,向量数量积的运算及计算公式,向量投影的定义及计算公式.

 阅读快车系列答案
阅读快车系列答案| 月份 | 9 | 10 | 11 | 12 | 1 |
| 历史(x 分) | 79 | 81 | 83 | 85 | 87 |
| 政治(y 分) | 77 | 79 | 79 | 82 | 83 |
(Ⅱ)一般来说,学生的历史成绩与政治成绩有较强的线性相关关系,根据上表提供的数据,求两个变量x,y的线性回归方程.
参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n\overline{x}2}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$,$\overline{x}$,$\overline{y}$表示样本均值.
| A. | g(x)为奇函数 | B. | 关于直线$x=\frac{π}{2}$对称 | ||
| C. | 关于点(π,0)对称 | D. | 在$(-\frac{π}{6},\frac{π}{4})$上递增 |
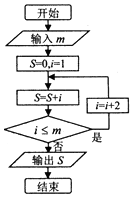
| A. | 4 | B. | 6 | C. | 7 | D. | 8 |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{2e}$ | C. | $\frac{1}{e}$ | D. | $\frac{1}{{e}^{2}}$ |