题目内容
6.已知定义在R上的函数满足f(x)+2f′(x)>0恒成立,且f(2)=$\frac{1}{e}$(e为自然对数的底数),则不等式ex•f(x)-e${\;}^{\frac{x}{2}}$>0的解集为(2,+∞).分析 令F(x)=${e}^{\frac{x}{2}}$f(x),从而求导F′(x),从而由导数求解不等式.
解答 解:定义在R上的函数满足f(x)+2f′(x)>0恒成立,
令F(x)=${e}^{\frac{x}{2}}$f(x),
则F′(x)=$\frac{1}{2}$${e}^{\frac{x}{2}}$[f(x)+2f′(x)]>0,
故F(x)是R上的单调增函数,
而F(2)=e1f(2)=1,
故不等式exf(x)>${e}^{\frac{x}{2}}$(其中e为自然对数的底数)的解集为(2,+∞);
故答案为:(2,+∞).
点评 本题考查了导数的综合应用及利用函数求解不等式,属于中档题.

练习册系列答案
相关题目
16.执行如图所示的程序框图,则输出S=( )
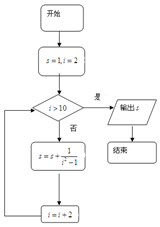

| A. | $\frac{5}{11}$ | B. | $\frac{13}{9}$ | C. | $\frac{16}{11}$ | D. | $\frac{17}{9}$ |
11.已知函数$f(x)=3sin(ωx+\frac{π}{3})$的最小正周期为π,将函数f(x)的图象向右平移$\frac{π}{6}$个所得图象对应的函数为y=g(x),则关于函数为y=g(x)的性质,下列说法不正确的是( )
| A. | g(x)为奇函数 | B. | 关于直线$x=\frac{π}{2}$对称 | ||
| C. | 关于点(π,0)对称 | D. | 在$(-\frac{π}{6},\frac{π}{4})$上递增 |