题目内容
3.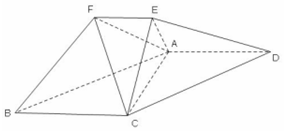 在如图所示的几何体中,平面ACE⊥平面ABCD,四边形ABCD 为平行四边形,
在如图所示的几何体中,平面ACE⊥平面ABCD,四边形ABCD 为平行四边形,∠CAD=90°,EF∥BC,EF=$\frac{1}{2}$BC,AC=$\sqrt{2}$,AE=EC=1.
(1)求证:CE⊥AF;
(2)若三棱锥F-ACD 的体积为$\frac{1}{3}$,求点D 到平面ACF 的距离.
分析 (1)推导出AD⊥平面AEC,从而AD⊥CE,由勾股定理得AE⊥EC,从而CE⊥平面ADEF,由此能证明CE⊥AF.
(2)设AC的中点为G,连接EG,推导出点F到面ABCD的距离等于点E到面ABCD的距离,由VF-ACD=VE-ACD,能求出点D到平面ACF的距离.
解答 证明:(1)∵平面ACE⊥平面ABCD,且平面ACE∩平面ABCD=AC,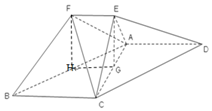
∵AD⊥AC,∴AD⊥平面AEC…(1分)
∵CE?平面AEC,∴AD⊥CE,…(2分)
又$AC=\sqrt{2},AE=EC=1$,∴AC2=AE2+CE2,∴AE⊥EC…(3分)
∵EF∥BC,BC∥AD,∴EF∥AD即A、D、E、F共面,…(4分)
又AE∩AD=D,∴CE⊥平面ADEF,…(5分)
∵AF?面ADEF,∴CE⊥AF.…(6分)
解:(2)设AC的中点为G,连接EG,
∵AE=CE,∴EG⊥AC
∵平面ACE⊥平面ABCD,且平面ACE∩平面ABCD=AC,
∴EG⊥平面ABCD∵EF∥BC,EF?平面ABCD,
∴点F到面ABCD的距离等于点E到面ABCD的距离,即EG…(7分)
∴${V_{F-ACD}}={V_{E-ACD}}=\frac{1}{3}{S_{△ACD}}•EG=\frac{1}{3}$…(8分)
${S_{△ACD}}=\frac{1}{2}AC•AD=\frac{1}{2}•\sqrt{2}•AD$,$EG=\frac{1}{2}AC=\frac{{\sqrt{2}}}{2}$
∴${V_{F-ACD}}=\frac{1}{3}•\frac{1}{2}•\sqrt{2}•AD•\frac{{\sqrt{2}}}{2}=\frac{1}{3}$,所以AD=2…(9分)
∴BC=AD=2,$EF=\frac{1}{2}BC=1$,$FA=FC=\sqrt{A{E^2}+E{F^2}}=\sqrt{2}$,
所以${S_{△FAC}}=\frac{1}{2}\sqrt{2}•\sqrt{2}•sin{60^0}=\frac{{\sqrt{3}}}{2}$…(10分)
设点D到平面ACF的距离为d,则$\frac{1}{3}{S_{△FAC}}•d=\frac{1}{3}$,…(11分)
解得$d=\frac{{2\sqrt{3}}}{3}$,所以点D到平面ACF的距离$\frac{{2\sqrt{3}}}{3}$.…(12分)
点评 本题考查线线垂直的证明,考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

 名校课堂系列答案
名校课堂系列答案| A. | g(x)为奇函数 | B. | 关于直线$x=\frac{π}{2}$对称 | ||
| C. | 关于点(π,0)对称 | D. | 在$(-\frac{π}{6},\frac{π}{4})$上递增 |
 某校某次N名学生的学科能力测评成绩(满分120分)的频率分布直方图如下,已知分数在100-110的学生数有21人(1)求总人数N和分数在110-115分的人数n.;
某校某次N名学生的学科能力测评成绩(满分120分)的频率分布直方图如下,已知分数在100-110的学生数有21人(1)求总人数N和分数在110-115分的人数n.;(2)现准备从分数在110-115的n名学生(女生占$\frac{1}{3}$)中选3位分配给A老师进行指导,设随机变量ξ表示选出的3位学生中女生的人数,求ξ的分布列与数学期望Eξ;
(3)为了分析某个学生的学习状态,对其下一阶段的学习提供指导建议,对他前7次考试的数学成绩x、物理成绩y进行分析,该生7次考试成绩如表
| 数学(x) | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
| 物理(y) | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
附:对于一组数据(x1,y1),(x2,y2),…,(xn,yn),其回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$的斜率和截距的最小二乘估计分别为$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i-}\overline{x})^{2}}$,$\stackrel{∧}{a}=\overline{y}-\stackrel{∧}{b}\overline{x}$.