题目内容
设数列{an}的前n项和为Sn,a1=1,Sn=nan-2n(n-1).
(1)求数列{an}的通项公式an;
(2)设数列{ }的前n项和为Tn,求证:
}的前n项和为Tn,求证: ≤Tn<
≤Tn< .
.
(1)解 由Sn=nan-2n(n-1)得
an+1=Sn+1-Sn=(n+1)an+1-nan-4n,
即an+1-an=4.
∴数列{an}是以1为首项,4为公差的等差数列,
∴an=4n-3.
 又易知Tn单调递增,
又易知Tn单调递增,
故Tn≥T1= ,得
,得 ≤Tn<
≤Tn< .
.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
铁矿石A和B的含铁率a,冶炼每万吨铁矿石的CO2的排放量b及每万吨铁矿石的价格c如下表:
|
| a | b/万吨 | c/百万元 |
| A | 50% | 1 | 3 |
| B | 70% | 0.5 | 6 |
某冶炼厂至少要生产1.9(万吨)铁,若要求CO2的排放量不超过2(万吨),则购买铁矿石的最少费用为________(百万元).
 展开式中各项系数之和为32,则该展开式中含
展开式中各项系数之和为32,则该展开式中含 的项的系数为
的项的系数为 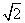 -1与
-1与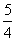 ,则S5等于( )
,则S5等于( ) 则z=3x+2y的最大值是( )
则z=3x+2y的最大值是( ) B.ω=
B.ω= ,θ=
,θ= D.ω=2,θ=
D.ω=2,θ=