题目内容
1.设Sn为各项不相等的等差数列an的前n 项和,已知a3a8=3a11,S3=9.(1)求数列{an}的通项公式;
(2)求数列{$\frac{1}{{{a_n}{a_{n+1}}}}$}的前n 项和Tn.
分析 (1)利用等差数列的通项公式与求和公式即可得出.
(2)利用“裂项求和”方法即可得出.
解答 解:(1)设{an}的公差为d,则由题意知$\left\{{\begin{array}{l}{({{a_1}+2d})({{a_1}+7d})=3({{a_1}+10d})}\\{3{a_1}+\frac{3×2}{2}d=9}\end{array}}\right.$…(2分)
解得$\left\{{\begin{array}{l}{d=0}\\{{a_1}=3}\end{array}}\right.$(舍去)或$\left\{{\begin{array}{l}{d=1}\\{{a_1}=2}\end{array}}\right.$,…(4分)
∴an=2+(n-1)×1=n+1…(6分)
(2)∵$\frac{1}{{{a_n}{a_{n+1}}}}=\frac{1}{{({n+1})({n+2})}}=\frac{1}{n+1}-\frac{1}{n+2}$,…(8分)
∴${T_n}=\frac{1}{{{a_1}{a_2}}}+\frac{1}{{{a_2}{a_3}}}+…+\frac{1}{{{a_n}{a_{n-1}}}}$…(9分)
=$({\frac{1}{2}-\frac{1}{3}})+({\frac{1}{3}-\frac{1}{5}})+…+({\frac{1}{n+1}-\frac{1}{n+2}})$.
=$\frac{1}{2}-\frac{1}{n+2}=\frac{n}{{2({n+2})}}$…(12分)
点评 本题考查了“裂项求和方法”、等差数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
12.已知命题p,q是简单命题,则“¬p是假命题”是“p∨q是真命题”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
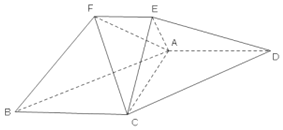 在如图所示的几何体中,平面ACE⊥平面ABCD,四边形ABCD 为平行四边形,
在如图所示的几何体中,平面ACE⊥平面ABCD,四边形ABCD 为平行四边形,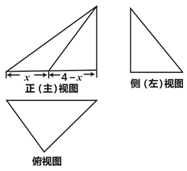 已知三棱锥的外接球的表面积为25π,该三棱锥的三视图如图所示,三个视图的外轮廓都是直角三角形,则其侧视图面积的最大值为3.
已知三棱锥的外接球的表面积为25π,该三棱锥的三视图如图所示,三个视图的外轮廓都是直角三角形,则其侧视图面积的最大值为3.