题目内容
11.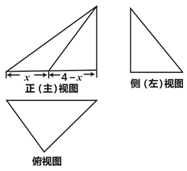 已知三棱锥的外接球的表面积为25π,该三棱锥的三视图如图所示,三个视图的外轮廓都是直角三角形,则其侧视图面积的最大值为3.
已知三棱锥的外接球的表面积为25π,该三棱锥的三视图如图所示,三个视图的外轮廓都是直角三角形,则其侧视图面积的最大值为3.
分析 由三棱锥的外接球的表面积为25π,可知外接圆半径R=5,即主视图的斜边长为5,可得高为3.设俯视图三角形的边长为a,b,可得a2+b2=42,设侧视图的底边为m,利用体积法,则有4m=ab,侧视图面积的最大值S=$\frac{1}{2}•$3m,利用基本不等式即可求解.
解答 解:三棱锥的外接球的表面积为25π,可知外接圆半径R=5,
三个视图的外轮廓都是直角三角形,可得主视图的斜边长为5,底边是4,则高为3.
设俯视图三角形的边长为a,b,可得a2+b2=42,
设侧视图的底边为m,利用体积法,则有4m=ab,
∵16=a2+b2≥2ab,解得:ab≤8,
又∵4m=ab,
∴m≤2
侧视图面积的S=$\frac{1}{2}$•3m≤3.
故答案为3.
点评 本题主要考查了三棱锥边长与外接圆的关系的建立和三视图的认识和理解,利用条件建立不等式关系是关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
2.大数据时代出现了滴滴打车服务,二胎政策的放开使得家庭中有两个小孩的现象普遍存在,某城市关系要好的A,B,C,D四个家庭各有两个小孩共8人,准备使用滴滴打车软件,分乘甲、乙两辆汽车出去游玩,每车限坐4名(乘同一辆车的4名小孩不考虑位置),其中A户家庭的孪生姐妹需乘同一辆车,则乘坐甲车的4名小孩恰有2名来自于同一个家庭的乘坐方式共有( )
| A. | 18种 | B. | 24种 | C. | 36种 | D. | 48种 |
19.已知函数F(x)=xf(x),f(x)满足f(x)=f(-x),且当x∈(-∞,0]时,F'(x)<0成立,若$a={2^{0.1}}•f({{2^{0.1}}}),b=ln2•f({ln2}),c={log_2}\frac{1}{8}•f({{{log}_2}\frac{1}{8}})$,则a,b,c的大小关系是( )
| A. | a>b>c | B. | c>a>b | C. | c>b>a | D. | a>c>b |
6.若集合A={x|log4x≤$\frac{1}{2}$},B={x|(x+3)( x-1)≥0},则A∩(∁RB)=( )
| A. | (0,1] | B. | (0,1) | C. | [1,2] | D. | [0,1] |
3.已知角θ的顶点与原点重合,始边与x轴的正半轴重合,终边在直线$y=-\sqrt{3}x$上,则sin2θ=( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
11.已知全集U=R,M={x|y=lg(1-$\frac{2}{x}$)},N={x|y=$\sqrt{x-1}$},则N∩(∁UM)=( )
| A. | ∅ | B. | [1,2] | C. | [0,2] | D. | [2,+∞) |