题目内容
6.已知曲线C 的参数方程为$\left\{\begin{array}{l}x=2+\sqrt{5}cosα\\ y=1+\sqrt{5}sinα\end{array}\right.$(α为参数),以直角坐标系原点O 为极点,x 轴正半轴为极轴建立极坐标系.(Ⅰ)求曲线C 的极坐标方程;
(Ⅱ)设l1:θ=$\frac{π}{6}$,l2:θ=$\frac{π}{3}$,若l 1、l2与曲线C 相交于异于原点的两点 A、B,求△AOB的面积.
分析 (Ⅰ)将C参数方程化为普通方程,利用$\left\{\begin{array}{l}x=ρcosθ\\ y=ρsinθ\end{array}\right.$代入,可得曲线C 的极坐标方程.
(Ⅱ)法一:利用参数的几何意义,求|OB|,|OA|,∠AOB=60°,即可求△AOB的面积,
法二:在平面直角坐标系中,根据l1:θ=$\frac{π}{6}$,l2:θ=$\frac{π}{3}$,求出方程与圆C求解交点A和B,|OB|,|OA|,∠AOB=60°,即可求△AOB的面积,
解答 解:(Ⅰ)∵曲线C的参数方程为$\left\{\begin{array}{l}x=2+\sqrt{5}cosα\\ y=1+\sqrt{5}sinα\end{array}\right.$(α为参数),利用sin2α+cos2α=1,
$\sqrt{5}sinα=x-2$,$\sqrt{5}cosα$=y-1,可得:(x-2)2+(y-1)2=5.
∴曲线C的普通方程为(x-2)2+(y-1)2=5.
将$\left\{\begin{array}{l}x=ρcosθ\\ y=ρsinθ\end{array}\right.$代入并化简得:ρ=4cosθ+2sinθ
即曲线C的极坐标方程为ρ=4cosθ+2sinθ.
(Ⅱ)解法一:在极坐标系中,C:ρ=4cosθ+2sinθ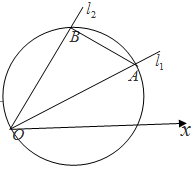
∴由$\left\{{\begin{array}{l}{θ=\frac{π}{6}}\\{ρ=4cosθ+2sinθ}\end{array}}\right.$得到$|{OA}|=2\sqrt{3}+1$;
同理$|{OB}|=2+\sqrt{3}$.
又∵$∠AOB=\frac{π}{6}$
∴${S_{△AOB}}=\frac{1}{2}|{OA}|•|{OB}|sin∠AOB=\frac{{8+5\sqrt{3}}}{4}$.
即△AOB的面积为$\frac{{8+5\sqrt{3}}}{4}$.…(10分)
解法二:在平面直角坐标系中,C:(x-2)2+(y-1)2=5
l1:θ=$\frac{π}{6}$,l2:θ=$\frac{π}{3}$,可得${l_1}:y=\frac{{\sqrt{3}}}{3}x$,${l_2}:y=\sqrt{3}x$
∴由$\left\{{\begin{array}{l}{y=\frac{{\sqrt{3}}}{3}x}\\{{{({x-2})}^2}+{{({y-1})}^2}=5}\end{array}}\right.$得$A({\frac{{6+\sqrt{3}}}{2},\frac{{2\sqrt{3}+1}}{2}})$
∴$|{OA}|=2\sqrt{3}+1$
同理$B({\frac{{2+\sqrt{3}}}{2},\frac{{2\sqrt{3}+3}}{2}})$
∴$|{OA}|=2\sqrt{3}+1$,$|{OB}|=2+\sqrt{3}$
又∵$∠AOB=\frac{π}{6}$
∴${S_{△AOB}}=\frac{1}{2}|{OA}|•|{OB}|sin∠AOB=\frac{{8+5\sqrt{3}}}{4}$
即△AOB的面积为$\frac{{8+5\sqrt{3}}}{4}$.
点评 本题主要考查了参数方程,极坐标方程与普通方程的换算.参数方程的几何意义的运用.属于中档题.

| 是否愿意提供志愿者服务 性别 | 愿意 | 不愿意 |
| 男生 | 25 | 5 |
| 女生 | 15 | 15 |
(2)在(1)中抽取出的8人中任选3人,求被抽中的女生人数的分布列和数学期望.
| A. | 向右平移$\frac{π}{4}$个单位长度 | B. | 向右平移$\frac{π}{12}$个单位长度 | ||
| C. | 向左平移$\frac{π}{4}$个单位长度 | D. | 向左平移$\frac{π}{12}$个单位长度 |
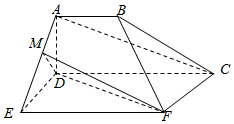 如图,空间几何体ADE-BCF中,四边形ABCD是梯形,四边形CDEF
如图,空间几何体ADE-BCF中,四边形ABCD是梯形,四边形CDEF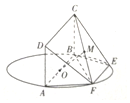 如图,AB为圆O的直径,点E,F在圆O上,AB∥EF,矩形ABCD所在的平面和圆(x-1)2+y2=1所在的平面互相垂直,且AB=2,AD=EF=1,∠BAF=60°.
如图,AB为圆O的直径,点E,F在圆O上,AB∥EF,矩形ABCD所在的平面和圆(x-1)2+y2=1所在的平面互相垂直,且AB=2,AD=EF=1,∠BAF=60°.