题目内容
10.若实数x,y满足约束条件$\left\{\begin{array}{l}{2x+y≤4}\\{x-y≥1}\\{x-2y≤2}\end{array}\right.$,则目标函数z=3x+y的最大值为( )| A. | 6 | B. | $\frac{17}{3}$ | C. | $\frac{20}{3}$ | D. | -1 |
分析 先画出约束条件的可行域,再求出可行域中各角点的坐标,将各点坐标代入目标函数的解析式,分析后易得目标函数z=3x+y的最大值.
解答 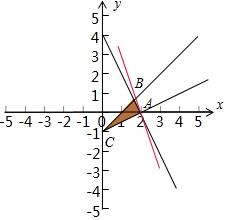 解:由约束条件$\left\{\begin{array}{l}{2x+y≤4}\\{x-y≥1}\\{x-2y≤2}\end{array}\right.$得如图所示的三角形区域,
解:由约束条件$\left\{\begin{array}{l}{2x+y≤4}\\{x-y≥1}\\{x-2y≤2}\end{array}\right.$得如图所示的三角形区域,
三个顶点坐标为A(2,0),$\left\{\begin{array}{l}{2x+y-4=0}\\{x-y-1=0}\end{array}\right.$解得B($\frac{5}{3}$,$\frac{2}{3}$),C(0,-1)
将三个代入z=3x+y得z的值分别为6,$\frac{17}{3}$,-1,
直线z=3x+y过点A (2,0)时,z取得最大值为6;
故选:A.
点评 在解决线性规划的小题时,我们常用“角点法”,其步骤为:①由约束条件画出可行域⇒②求出可行域各个角点的坐标⇒③将坐标逐一代入目标函数⇒④验证,求出最优解.

练习册系列答案
相关题目
1.已知函数f(x)=$\left\{\begin{array}{l}{\frac{1}{6}x+2,x>a}\\{{x}^{2}+3x+2,x≤a}\end{array}\right.$,函数g(x)=f(x)-ax,恰有三个不同的零点,则a的取值范围是( )
| A. | ($\frac{1}{6}$,3-2$\sqrt{2}$) | B. | ($\frac{1}{6}$,$\frac{3}{2}$) | C. | (-∞,3-2$\sqrt{2}$) | D. | (3-2$\sqrt{2}$,+∞) |
18.设全集为R,集合A={x|x2+3x≤0},则∁RA=( )
| A. | {x|x<-3或x>0} | B. | {x|x≤3或x≥0} | C. | {x|-3<x<0} | D. | {x|-3≤x≤0} |
1.命题甲:对任意x∈(a,b),有f′(x)>0;命题乙:f(x)在(a,b)内是单调递增的,则甲是乙的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
18.已知抛物线C:y2=8x的焦点为F,准线为l,P是l上一点,直线PF与曲线相交于M,N两点,若$\overrightarrow{PF}$=3$\overrightarrow{MF}$,则|MN|=( )
| A. | $\frac{21}{2}$ | B. | $\frac{32}{3}$ | C. | 10 | D. | 11 |
19.已知a=0.30.3,b=1.20.3,c=log1.20.3,则a,b,c的大小关系为( )
| A. | c<a<b | B. | c<b<a | C. | a<b<c | D. | a<c<b |
 某企业拟用10万元投资甲、乙两种商品.已知各投入x万元,甲、乙两种商品分别可获得y1,y2万元的利润,利润曲线${P_1}:{y_1}=a{x^n}$,P2:y2=bx+c,如图所示.
某企业拟用10万元投资甲、乙两种商品.已知各投入x万元,甲、乙两种商品分别可获得y1,y2万元的利润,利润曲线${P_1}:{y_1}=a{x^n}$,P2:y2=bx+c,如图所示.