题目内容
15.已知平面内三个单位向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$,<$\overrightarrow{OA}$,$\overrightarrow{OB}$>=60°,若$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$,则m+n的最大值是$\frac{2\sqrt{3}}{3}$.分析 将$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$两边平方后整理得(m+n)2-1=mn,再由基本不等式可得x+y的最大值.
解答 解:由已知条件$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$,
两边平方可得1=m2+mn+n2=(m+n)2-mn,
∴(m+n)2-1=mn,根据向量加法的平行四边形法则,判断出m,n>0,
∴(m+n)2-1=mn≤$\frac{1}{4}$(m+n)2,
∴$\frac{3}{4}(m+n)^{2}≤1$,则m+n≤$\frac{2\sqrt{3}}{3}$,
即m+n的最大值为$\frac{2\sqrt{3}}{3}$.
故答案为:$\frac{2\sqrt{3}}{3}$
点评 本题考查的知识点是平面向量的基本定理,基本不等式,其中根据已知分析出(m+n)2-1=mn是解答的关键,属中档题.

练习册系列答案
相关题目
5.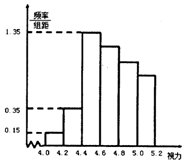 某校高一共录取新生1000名,为了解学生视力情况,校医随机抽取了100名学生进行视力测试,并得到如下频率分布直方图.
某校高一共录取新生1000名,为了解学生视力情况,校医随机抽取了100名学生进行视力测试,并得到如下频率分布直方图.
(Ⅰ)若视力在4.6~4.8的学生有24人,试估计高一新生视力在4.8以上的人数;
(Ⅱ)校医发现学习成绩较高的学生近视率较高,又在抽取的100名学生中,对成绩在前50名的学生和其他学生分别进行统计,得到如右数据,根据这些数据,校医能否有超过95%的把握认为近视与学习成绩有关?
(Ⅲ)用分层抽样的方法从(Ⅱ)中27名不近视的学生中抽出6人,再从这6人中任抽2人,其中抽到成绩在前50名的学生人数为ξ,求ξ的分布列和数学期望.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
 某校高一共录取新生1000名,为了解学生视力情况,校医随机抽取了100名学生进行视力测试,并得到如下频率分布直方图.
某校高一共录取新生1000名,为了解学生视力情况,校医随机抽取了100名学生进行视力测试,并得到如下频率分布直方图.(Ⅰ)若视力在4.6~4.8的学生有24人,试估计高一新生视力在4.8以上的人数;
| 1~50名 | 951~1000名 | |
| 近视 | 41 | 32 |
| 不近视 | 9 | 18 |
(Ⅲ)用分层抽样的方法从(Ⅱ)中27名不近视的学生中抽出6人,再从这6人中任抽2人,其中抽到成绩在前50名的学生人数为ξ,求ξ的分布列和数学期望.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
6.已知$\frac{1-ai}{1+i}=b-i$(a,b∈R),其中i为虚数单位,则a+b=( )
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
10.若实数x,y满足约束条件$\left\{\begin{array}{l}{2x+y≤4}\\{x-y≥1}\\{x-2y≤2}\end{array}\right.$,则目标函数z=3x+y的最大值为( )
| A. | 6 | B. | $\frac{17}{3}$ | C. | $\frac{20}{3}$ | D. | -1 |
6.在等差数列{an}中,若a2+a8=12,则a1-a3+a7的值为( )
| A. | 1 | B. | 2 | C. | 4 | D. | 6 |