题目内容
18.已知抛物线C:y2=8x的焦点为F,准线为l,P是l上一点,直线PF与曲线相交于M,N两点,若$\overrightarrow{PF}$=3$\overrightarrow{MF}$,则|MN|=( )| A. | $\frac{21}{2}$ | B. | $\frac{32}{3}$ | C. | 10 | D. | 11 |
分析 先根据题意写出直线的方程,再将直线的方程与抛物线y2=8x的方程组成方程组,消去y得到关于x的二次方程,最后利用根与系数的关系结合抛物线的定义即可求线段MN的长.
解答 解:抛物线C:y2=8x的焦点为F(2,0),准线为l:x=-2,设M(x1,y1),N(x2,y2),M,N到准线的距离分别为dM,dN,
由抛物线的定义可知|MF|=dM=x1+1,|NF|=dN=x2+1,于是|MN|=|MF|+|NF|=x1+x2+4.
∵$\overrightarrow{PF}$=3$\overrightarrow{MF}$,
∴直线AB的斜率为±$\sqrt{3}$,
∵F(2,0),
∴直线PF的方程为y=±$\sqrt{3}$(x-2),
将y=±$\sqrt{3}$(x-2),代入方程y2=8x,得3(x-2)2=8x,化简得3x2-20x+12=0,
∴x1+x2=$\frac{20}{3}$,于是|MN|=|MF|+|NF|=x1+x2+4=$\frac{20}{3}$+4=$\frac{32}{3}$.
故选:B.
点评 本题考查抛物线的定义和性质,考查向量知识的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
10.若实数x,y满足约束条件$\left\{\begin{array}{l}{2x+y≤4}\\{x-y≥1}\\{x-2y≤2}\end{array}\right.$,则目标函数z=3x+y的最大值为( )
| A. | 6 | B. | $\frac{17}{3}$ | C. | $\frac{20}{3}$ | D. | -1 |
6.在等差数列{an}中,若a2+a8=12,则a1-a3+a7的值为( )
| A. | 1 | B. | 2 | C. | 4 | D. | 6 |
13.双曲线实半轴长为2,焦点为(-3,0)、(3,0),则该双曲线为( )
| A. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{9}$=1 | B. | $\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1 | D. | $\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{5}$=1 |
7.已知向量$\overrightarrow a=(x-5,3),\overrightarrow b=(2,x)$且$\overrightarrow a⊥\overrightarrow b$则x=2.
8.若等边△ABC的边长为3,平面内一点M满足$\overrightarrow{CM}=\frac{1}{3}\overrightarrow{CB}+\frac{1}{2}\overrightarrow{CA}$,则$\overrightarrow{AM}•\overrightarrow{MB}$的值为( )
| A. | 2 | B. | $-\frac{15}{2}$ | C. | $\frac{15}{2}$ | D. | -2 |
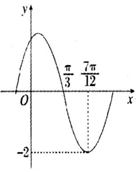 函数$f(x)=Asin({ωx+φ})({A>0,ω>0,|φ|≤\frac{π}{2}})$的部分图象如图所示,其中$f({\frac{π}{3}})=0,f({\frac{7π}{12}})=-2$,给出下列结论:
函数$f(x)=Asin({ωx+φ})({A>0,ω>0,|φ|≤\frac{π}{2}})$的部分图象如图所示,其中$f({\frac{π}{3}})=0,f({\frac{7π}{12}})=-2$,给出下列结论: