题目内容
1．命题甲：对任意x∈（a，b），有f′（x）＞0；命题乙：f（x）在（a，b）内是单调递增的，则甲是乙的（ ）| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
分析 根据充分条件和必要条件的定义结合函数单调性与导函数符号之间的关系，进行判断即可．
解答 解：对任意x∈（a，b），有f′（x）＞0，则f（x）在（a，b）内是单调递增的，
则甲是乙的充分条件，
f（x）在（a，b）内是单调递增的，则对任意x∈（a，b），有f′（x）≥0，
则甲是乙的不必要条件，
故甲是乙的充分不必要条件，
故选：A
点评 本题考查的知识点是充要条件，利用导数研究函数的单调性，正确理解充要条件的概念是解答的关键．
练习册系列答案
相关题目
12．已知函数f（x）=$\left\{\begin{array}{l}{{2}^{x}，x＜0}\\{m-{x}^{2}，x≥0}\end{array}\right.$，给出下列两个命题：命题p：?m∈（-∞，0），方程f（x）=0有实数解；命题q：当m=$\frac{1}{4}$时，f（f（-1））=0，则下列命题为真命题的是（ ）
| A． | p∧q | B． | （￢p）∧q | C． | p∧（￢q） | D． | （￢p）∧（￢q） |
10．若实数x，y满足约束条件$\left\{\begin{array}{l}{2x+y≤4}\\{x-y≥1}\\{x-2y≤2}\end{array}\right.$，则目标函数z=3x+y的最大值为（ ）
| A． | 6 | B． | $\frac{17}{3}$ | C． | $\frac{20}{3}$ | D． | -1 |
6．在等差数列{an}中，若a2+a8=12，则a1-a3+a7的值为（ ）
| A． | 1 | B． | 2 | C． | 4 | D． | 6 |
13．双曲线实半轴长为2，焦点为（-3，0）、（3，0），则该双曲线为（ ）
| A． | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{9}$=1 | B． | $\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{9}$=1 | C． | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1 | D． | $\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{5}$=1 |
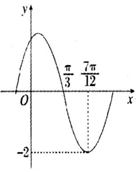函数$f（x）=Asin（{ωx+φ}）（{A＞0，ω＞0，|φ|≤\frac{π}{2}}）$的部分图象如图所示，其中$f（{\frac{π}{3}}）=0，f（{\frac{7π}{12}}）=-2$，给出下列结论：