题目内容
17.在△ABC中,角A,B,C的对边分别为a,b,c,若a=4,sinA=2sinB,则b=( )| A. | 8 | B. | 4 | C. | 2 | D. | 1 |
分析 由已知利用正弦定理即可计算得解.
解答 解:∵a=4,sinA=2sinB,
∴由正弦定理$\frac{a}{sinA}=\frac{b}{sinB}$,可得:b=$\frac{asinB}{sinA}$=$\frac{4sinB}{2sinB}$=2.
故选:C.
点评 本题主要考查了正弦定理在解三角形中的应用,考查了转化思想,属于基础题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
8.给出如下四个命题,其中正确的命题为( )
| A. | 若“p且q”为假命题,则p、q均为假命题 | |
| B. | 命题“若a>b,则2a>2b-1”的否命题为“若a≤b,则2a≤2b-1” | |
| C. | “?x∈R,x2+1≥1”的否定是“?x∈R,x2+1≤1” | |
| D. | 在△ABC中,“A>B”是“sinA>sinB”的充分不必要条件 |
5.已知f(x),g(x)定义在同一区间上,f(x)是增函数,g(x)是减函数,且g(x)≠0,则( )
| A. | f(x)+g(x) 为减函数 | B. | f(x)-g(x)为增函数 | C. | f(x)•g(x)是减函数 | D. | $\frac{f(x)}{g(x)}$ 是增函数 |
12.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点为F(-c,0),M、N在双曲线C上,O是坐标原点,若四边形OFMN为平行四边形,且四边形OFMN的面积为$\sqrt{2}$cb,则双曲线C的离心率为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
9.若不等式mx2+x+n>0的解集是{x|-$\frac{1}{3}$<x<$\frac{1}{2}$},则m,n分别是( )
| A. | 6,-1 | B. | -6,-1 | C. | 6,1 | D. | -6,1 |
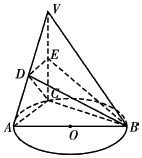 如图AB是圆O的直径,点C是弧AB上一点,VC垂直圆O所在平面,D,E分别为VA,VC的中点.
如图AB是圆O的直径,点C是弧AB上一点,VC垂直圆O所在平面,D,E分别为VA,VC的中点.