Question

12．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左焦点为F（-c，0），M、N在双曲线C上，O是坐标原点，若四边形OFMN为平行四边形，且四边形OFMN的面积为$\sqrt{2}$cb，则双曲线C的离心率为（　　）

• A． $\sqrt{2}$
• B． 2
• C． 2$\sqrt{2}$
• D． 2$\sqrt{3}$

Answer 1

分析 设M（x₀，y₀），y₀＞0，由四边形OFMN为平行四边形，四边形OFMN的面积为$\sqrt{2}$cb，由x₀=-$\frac{c}{2}$，丨y₀丨=$\sqrt{2}$b，代入双曲线方程，由离心率公式，即可求得双曲线C的离心率．

解答 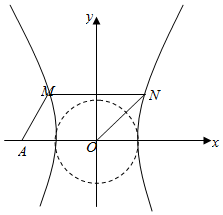解：双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）焦点在x轴上，
设M（x₀，y₀），y₀＞0，由四边形OFMN为平行四边形，
∴x₀=-$\frac{c}{2}$，
四边形OFMN的面积为$\sqrt{2}$cb，
∴丨y₀丨c=$\sqrt{2}$cb，即丨y₀丨=$\sqrt{2}$b，
∴M（-$\frac{c}{2}$，$\sqrt{2}$b），
代入双曲线可得：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1，整理得：$\frac{{c}^{2}}{4{a}^{2}}-2=1$，
由e=$\frac{c}{a}$，
∴e²=12，由e＞1，解得：e=2$\sqrt{3}$，
故选D．

点评 本题考查双曲线的标准方程，考查双曲线的离心率公式，考查计算能力，属于中档题．