题目内容
2.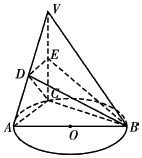 如图AB是圆O的直径,点C是弧AB上一点,VC垂直圆O所在平面,D,E分别为VA,VC的中点.
如图AB是圆O的直径,点C是弧AB上一点,VC垂直圆O所在平面,D,E分别为VA,VC的中点.(1)求证:DE⊥VB;
(2)若VC=CA=6,圆O的半径为5,求点E到平面BCD的距离.
分析 (1)利用直径对直角,得出AC⊥BC,再由直线VC⊥AC,证明AC⊥平面VBC,再由ED∥AC,得出ED⊥平面VBC,从而证明VB⊥DE;
(2)利用等体积法,得到VE-BC=VB-CDE,即可求出点点到平面BCD的距离.
解答 证明:(1)∵AB是⊙O的直径,点C是⊙O上的点,
∴AC⊥BC,
又直线VC垂直于⊙O所在的平面,
∴VC⊥AC,
又VC∩BC=C,∴AC⊥平面VBC;
又D、E分别是VA、VC的中点,
∴ED∥AC,
∴ED⊥平面VBC,
又VB?平面VBC,
∴VB⊥DE
(2)设点E到平面BCD 的距离为d,
由VE-BC=VB-CDE得$\frac{1}{3}$d•S△BCD=$\frac{1}{3}$×8×$\frac{1}{2}$×3×3=12
∵S△BCD=$\frac{1}{2}$×8×3$\sqrt{2}$=12$\sqrt{2}$
解得d=$\frac{3\sqrt{2}}{2}$
即点E到平面BCD的距离为$\frac{3\sqrt{2}}{2}$.
点评 本题考查了空间中的平行与垂直共线的应用问题,也考查了逻辑思维与空间想象能力,属于中档题.

练习册系列答案
相关题目
12.函数f(x)=$\left\{\begin{array}{l}{x+1(x≥0)}\\{{x}^{2}+2x+1(x<0)}\end{array}\right.$,若矩形ABCD的顶点A、D在x轴上,B、C在函数y=f(x)的图象上,且A(1,0),则点D的坐标为( )
| A. | (-2,0) | B. | (-1-$\sqrt{2}$,0) | C. | (-1,0) | D. | (-$\frac{1}{2}$,0) |
10.已知A、B是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的两个焦点,若在双曲线上存在点P满足2|$\overrightarrow{PA}$+$\overrightarrow{PB}$|≤|$\overrightarrow{AB}$|,则双曲线C的离心率e的取值范围是( )
| A. | 1<e≤2 | B. | e≥2 | C. | 1<e≤$\sqrt{2}$ | D. | e≥$\sqrt{2}$ |
11.正三棱柱ABC-A1B1C1中,若AC=$\sqrt{2}$AA1,则AB1与CA1所成角的大小为( )
| A. | 60° | B. | 105° | C. | 75° | D. | 90° |