题目内容
在△ABC中,已知a4+b4+c4=2c2(a2+b2),则C= .
考点:余弦定理
专题:解三角形
分析:a4+b4+c4=2c2(a2+b2),化为(a2+b2-c2)2=2a2b2,开方为a2+b2-c2=±
ab,再利用余弦定理即可得出.
| 2 |
解答:
解:∵a4+b4+c4=2c2(a2+b2),
∴(a2+b2)2-2c2(a2+b2)+c4=2a2b2,
∴(a2+b2-c2)2=2a2b2,
化为a2+b2-c2=±
ab,
由余弦定理可得:cosC=
=±
,
∵C∈(0,π),
∴C=
或
.
故答案为:
或
.
∴(a2+b2)2-2c2(a2+b2)+c4=2a2b2,
∴(a2+b2-c2)2=2a2b2,
化为a2+b2-c2=±
| 2 |
由余弦定理可得:cosC=
| a2+b2-c2 |
| 2ab |
| ||
| 2 |
∵C∈(0,π),
∴C=
| π |
| 4 |
| 3π |
| 4 |
故答案为:
| π |
| 4 |
| 3π |
| 4 |
点评:本题考查了乘法公式的应用、余弦定理解三角形,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=
,则函数g(x)=f(x)-x在区间[-5,5]上的零点之和为( )
|
| A、15 | B、16 | C、30 | D、32 |
| cos200 |
| sin200 |
| 3 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
在各项均为正数的等比数列{an}中,a2,
a3,a1成等比数列,则
的值为( )
| 1 |
| 2 |
| a5+a6 |
| a3+a4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
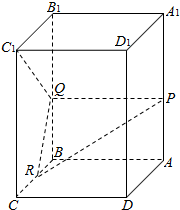 已知正四棱柱ABCD-A1B1C1D1,底面边长为
已知正四棱柱ABCD-A1B1C1D1,底面边长为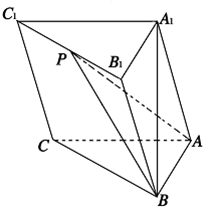 如图,在三棱柱ABC-A1B1C1中,AB⊥AC,AC⊥BB1,AB=A1B=AC=1,BB1=
如图,在三棱柱ABC-A1B1C1中,AB⊥AC,AC⊥BB1,AB=A1B=AC=1,BB1=