题目内容
在各项均为正数的等比数列{an}中,a2,
a3,a1成等比数列,则
的值为( )
| 1 |
| 2 |
| a5+a6 |
| a3+a4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:等比数列的通项公式
专题:等差数列与等比数列
分析:设等比数列{an}的公比为q,由题意和等比数列的通项公式列出方程,结合条件求出公比,利用等比数列的通项公式化简所求的式子,将q的值代入化简即可.
解答:
解:设等比数列{an}的公比为q,
因为a2,
a3,a1成等差数列,所以a3=a1+a2,
化简得q2-q-1=0,解得q=
,
因为数列的各项均为正数,所以q=
,
所以
=
=q2=(
)2=
,
故选:C.
因为a2,
| 1 |
| 2 |
化简得q2-q-1=0,解得q=
1±
| ||
| 2 |
因为数列的各项均为正数,所以q=
1+
| ||
| 2 |
所以
| a5+a6 |
| a3+a4 |
| a3q2+a3q3 |
| a3+a3q |
1+
| ||
| 2 |
3+
| ||
| 2 |
故选:C.
点评:本题考查等比数列的通项公式,以及方程思想,考查化简计算能力.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
质点运动规律为s=t2-3,则在时间(3,3+△t)中相应的平均速度为( )
| A、3 | B、6 | C、9 | D、12 |
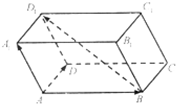 如图,四棱柱ABCD-A1B1C1D1的底面ABCD为平行四边形,已知
如图,四棱柱ABCD-A1B1C1D1的底面ABCD为平行四边形,已知| AB |
| a |
| AD |
| b |
| AA1 |
| c |
| a |
| b |
| c |
| BD1 |
A、
| ||||||
B、-
| ||||||
C、
| ||||||
D、-
|
已知A、B、C三点不共线,对平面ABC外的任一点O,下列条件中能确定定点M与点A、B、C一定共面的是( )
A、
| ||||||||||||||
B、
| ||||||||||||||
C、
| ||||||||||||||
D、
|