题目内容
求倾斜角为直线y=-
x+1的倾斜角的一半，且在y轴上的截距为-10的直线方程．
| 3 |
考点：直线的一般式方程
专题：直线与圆
分析：根据倾斜角的概念易知所求直线的倾斜角为60°，由斜截式方程可知，所求直线方程为y=
x-10．
| 3 |
解答：
解：∵直线y=-
x+1的斜率为-
，
∴直线y=-
x+1的倾斜角为120°，
∴所求直线的倾斜角为60°
∴k=
，
由斜截式方程可知，
所求直线方程为y=
x-10．
| 3 |
| 3 |
∴直线y=-
| 3 |
∴所求直线的倾斜角为60°
∴k=
| 3 |
由斜截式方程可知，
所求直线方程为y=
| 3 |
点评：本题考查直线倾斜角的概念和斜截式方程的应用，属于基础题．
练习册系列答案
相关题目
执行如图所示的程序框图，则输出结果S的值为（ ）
A、
| ||
| B、0 | ||
C、-
| ||
| D、-1 |
下列命题中，正确的是（ ）
| A、若a＞b，则ac2＞bc2 |
| B、若a+b＞a，则b＞0 |
| C、若b-a＞-a，则b＜0 |
| D、若ab＞0，则a＞0，且b＞0 |
在一个△ABC中，若a=2，b=2
，A=30°，那么B等于（ ）
| 3 |
| A、60° |
| B、60°或 120° |
| C、30° |
| D、30°或150° |
下列函数中，在其定义域内，既是奇函数又是减函数的是（ ）
A、f（x）=
| ||
| B、f（x）=-x3 | ||
| C、f（x）=-tan x | ||
D、f（x）=
|
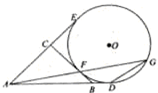如图，AD，AE，BC分别与圆切D，E，F于点，延长AF与圆O交于另一点G，给出下列三个结论：