题目内容
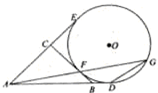如图，AD，AE，BC分别与圆切D，E，F于点，延长AF与圆O交于另一点G，给出下列三个结论：①AD+AE=AB+BC+CA
②△AFB～△ADG
③AF•AG=AD•AE
其中正确结论的序号是（ ）
| A、①② | B、②③ | C、①③ | D、①②③ |
考点：弦切角,与圆有关的比例线段
专题：直线与圆
分析：由切线性质，能推导出AD+AE=AB+BC+CA；连接FD，若△AFB～△ADG，则有∠ABF=∠DGF，不成立；由切割定理可得AF•AG=AD2=AD•AE．
解答：
解：在①中：由切线性质，得BD=BF，CF=CE，
∴AD+AE=AB+BC+CA，故①正确；
在②中：连接FD（如图），
若△AFB～△ADG，则有∠ABF=∠DGF．
通过图象结合圆的性质，得：
∠ABF=∠BFD+∠BDF=2∠DGF，不成立，故②错误；
在③中，由切线性质得AD=AE，
∴由切割定理可得AF•AG=AD2=AD•AE，故③正确．
故选：C．
在①中：由切线性质，得BD=BF，CF=CE，∴AD+AE=AB+BC+CA，故①正确；
在②中：连接FD（如图），
若△AFB～△ADG，则有∠ABF=∠DGF．
通过图象结合圆的性质，得：
∠ABF=∠BFD+∠BDF=2∠DGF，不成立，故②错误；
在③中，由切线性质得AD=AE，
∴由切割定理可得AF•AG=AD2=AD•AE，故③正确．
故选：C．
点评：本题考查命题真假的判断，是基础题，解题时要认真审题，注意圆的简单性质的合理运用．
练习册系列答案
相关题目
设f（x）=
，则f（f（2））=（ ）
|
| A、-1 | B、-2 | C、1 | D、2 |
已知不等式
＞0的解集为（-1，2），则二项式（ax-
）6展开式的常数项是（ ）
| x-2 |
| ax-1 |
| 1 |
| x2 |
| A、5 | B、-5 | C、15 | D、25 |
已知p：函数f（x）=|x+a|在（-∞，-1）上是单调函数；q：函数g（x）=loga（x+1）（a＞0且a≠1）在（-1，+∞）上是增函数，则￢p成立是q成立的（ ）
| A、充分不必要 |
| B、必要不充分 |
| C、充要条件 |
| D、既不充分也不必要 |
已知函数f（x）=
sinxcosx+
cos2x，若将其图象向右平移φ（φ＞0）个单位所得的图象关于原点对称，则φ的最小值为（ ）
| 3 |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|