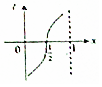题目内容
17.已知$sin(α-\frac{π}{12})=\frac{1}{3}$,则$cos(α+\frac{17π}{12})$的值等于( )| A. | $\frac{1}{3}$ | B. | $\frac{{2\sqrt{2}}}{3}$ | C. | $-\frac{1}{3}$ | D. | $-\frac{{2\sqrt{2}}}{3}$ |
分析 观察发现$\frac{π}{12}+\frac{17π}{12}=\frac{3}{2}π$,那么$cos(α+\frac{17π}{12})$=cos(α+$\frac{3π}{2}-\frac{π}{12}$)利用诱导公式求解即可.
解答 解:由$sin(α-\frac{π}{12})=\frac{1}{3}$,
则$cos(α+\frac{17π}{12})$=cos(α+$\frac{3π}{2}-\frac{π}{12}$)=sin(α-$\frac{π}{12}$)=$\frac{1}{3}$.
故选:A.
点评 本题主要考查诱导公式的灵活应用和构造思想,属于基本知识的考查.

练习册系列答案
相关题目
12.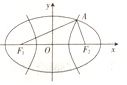 如图F1,F2是双曲线${C_1}:{x^2}-\frac{y^2}{8}=1$与椭圆C2的公共焦点,点A是C1,C2在第一象限内的公共点,若|F1F2|=|F1A|,则C2的离心率是( )
如图F1,F2是双曲线${C_1}:{x^2}-\frac{y^2}{8}=1$与椭圆C2的公共焦点,点A是C1,C2在第一象限内的公共点,若|F1F2|=|F1A|,则C2的离心率是( )
 如图F1,F2是双曲线${C_1}:{x^2}-\frac{y^2}{8}=1$与椭圆C2的公共焦点,点A是C1,C2在第一象限内的公共点,若|F1F2|=|F1A|,则C2的离心率是( )
如图F1,F2是双曲线${C_1}:{x^2}-\frac{y^2}{8}=1$与椭圆C2的公共焦点,点A是C1,C2在第一象限内的公共点,若|F1F2|=|F1A|,则C2的离心率是( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{5}$ |
9.已知函数f(x)是定义在R上的奇函数,当x≥0时,$f(x)=\frac{1}{2}(|x-1|+|x-2|-3)$,若?x∈R,f(x-a)≤f(x),则a的取值范围是( )
| A. | a≥3 | B. | -3≤a≤3 | C. | a≥6 | D. | -6≤a≤6 |
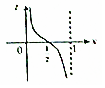
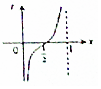
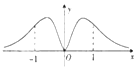
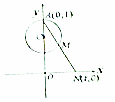 把周长为1的圆的圆心C放在y轴,顶点A(0,1),一动点M从A开始顺时针绕圆运动一周,记走过的弧长$\widehat{AM}$=x,直线AM与x轴交于点N(t,0),则函数t=f(x)的大致图象( )
把周长为1的圆的圆心C放在y轴,顶点A(0,1),一动点M从A开始顺时针绕圆运动一周,记走过的弧长$\widehat{AM}$=x,直线AM与x轴交于点N(t,0),则函数t=f(x)的大致图象( )