题目内容
9.已知函数f(x)是定义在R上的奇函数,当x≥0时,$f(x)=\frac{1}{2}(|x-1|+|x-2|-3)$,若?x∈R,f(x-a)≤f(x),则a的取值范围是( )| A. | a≥3 | B. | -3≤a≤3 | C. | a≥6 | D. | -6≤a≤6 |
分析 根据题意,由函数在x≥0时的解析式,将其用分段函数表示为f(x)=$\left\{\begin{array}{l}{-x,0≤x<1}\\{-1,1≤x≤2}\\{x-3,x>2}\end{array}\right.$,又由函数为奇函数,利用奇函数关于原点对称的性质可得f(x)的图象,进而分析可得a的取值范围,即可得答案.
解答 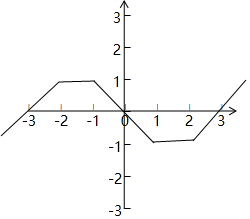 解:根据题意,当x≥0时,$f(x)=\frac{1}{2}(|x-1|+|x-2|-3)$=$\left\{\begin{array}{l}{-x,0≤x<1}\\{-1,1≤x≤2}\\{x-3,x>2}\end{array}\right.$,
解:根据题意,当x≥0时,$f(x)=\frac{1}{2}(|x-1|+|x-2|-3)$=$\left\{\begin{array}{l}{-x,0≤x<1}\\{-1,1≤x≤2}\\{x-3,x>2}\end{array}\right.$,
又由函数为奇函数,则其图象如图:
若?x∈R,f(x-a)≤f(x),
即点(x-a,f(x-a))在点(x,f(x))的下方或同一条水平线上,
必有a≥6,
故选:C.
点评 本题考查函数奇偶性的性质以及应用,涉及分段函数的性质,关键是依据题意,作出函数的图象.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.《九章算术•均输》中有如下问题:“今有五人分五钱,令上二人所得与下三人等,问各得几何.”其意思为“已知甲、乙、丙、丁、戊五人分5 钱,甲、乙两人所得与丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差数列,问五人各得多少钱?”(“钱”是古代的一种重量单位).这个问题中,乙所得为( )
| A. | $\frac{4}{3}$钱 | B. | $\frac{5}{4}$钱 | C. | $\frac{6}{5}$钱 | D. | $\frac{7}{6}$钱 |
20.已知函数f(x)=x2+$\frac{a}{x}$,则“0<a<2”是“函数f(x)在(1,+∞)上为增函数”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
17.已知$sin(α-\frac{π}{12})=\frac{1}{3}$,则$cos(α+\frac{17π}{12})$的值等于( )
| A. | $\frac{1}{3}$ | B. | $\frac{{2\sqrt{2}}}{3}$ | C. | $-\frac{1}{3}$ | D. | $-\frac{{2\sqrt{2}}}{3}$ |
14.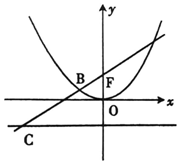 如图,过抛物线x2=2py(p>0)的焦点F的直线l交抛物线于AB,交其准线于点C,若|BC|=2|BF|,且|AF|=2,则p=( )
如图,过抛物线x2=2py(p>0)的焦点F的直线l交抛物线于AB,交其准线于点C,若|BC|=2|BF|,且|AF|=2,则p=( )
 如图,过抛物线x2=2py(p>0)的焦点F的直线l交抛物线于AB,交其准线于点C,若|BC|=2|BF|,且|AF|=2,则p=( )
如图,过抛物线x2=2py(p>0)的焦点F的直线l交抛物线于AB,交其准线于点C,若|BC|=2|BF|,且|AF|=2,则p=( )| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2-$\sqrt{2}$ |
1.下列命题中不正确的是( )
| A. | 如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥γ | |
| B. | 如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β | |
| C. | 如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β | |
| D. | 如果平面α⊥平面β,且直线l∥平面α,则直线l⊥平面β |
18.若1≤log2(x-y+1)≤2,|x-3|≤1,则x-2y的最大值与最小值之和是( )
| A. | 0 | B. | -2 | C. | 2 | D. | 6 |
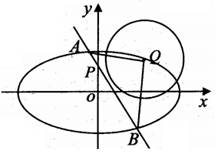 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,圆Q:x2+y2-4x-2y+3=0的圆心Q在椭圆C上,点P(0,1)到椭圆C的右焦点的距离为2.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,圆Q:x2+y2-4x-2y+3=0的圆心Q在椭圆C上,点P(0,1)到椭圆C的右焦点的距离为2.