题目内容

5．函数y=$\frac{{x}^{2}}{{e}^{|x|+1}}$（其中e为自然对数的底）的图象大致是（　　）
A．B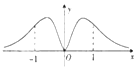．C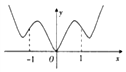．D．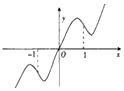

分析 利用函数的导数，求出函数的极大值，判断函数的图形即可．

解答 解：当x≥0时，函数y=$\frac{{x}^{2}}{{e}^{|x|+1}}$=$\frac{{x}^{2}}{{e}^{x+1}}$，y′=$\frac{2x-{x}^{2}}{{e}^{x+1}}$，有且只有一个极大值点是x=2，
故选：A．

点评 本题考查函数的导数的应用，函数的极值以及函数的图象的判断，考查分析问题解决问题的能力．

练习册系列答案
相关题目
15．下列命题中真命题是（　　）
A．$?x∈（{-∞，\frac{π}{4}}），tanx≤1$
B．设l，m表示不同的直线，α表示平面，若m∥l且m⊥α，则l∥α
C．利用计算机产生0和l之间的均匀随机数m，则事件“3m-1≥0”发生的概率为$\frac{1}{3}$
D．“a＞0，b＞0”是“$\frac{b}{a}+\frac{a}{b}$≥2”的充分不必要条件
16．执行如图所示的程序框图，输出的S值为（　　）
A．3025B．-3024C．-3025D．-6050
13．在直角坐标系xOy中，直线l1的方程为y=$\sqrt{3}$x，曲线C的参数方程为$\left\{\begin{array}{l}x=1+\sqrt{3}cosφ\\ y=\sqrt{3}sinφ\end{array}$（φ是参数，0≤φ≤π）．以O为极点，x轴的非负半轴为极轴建立极坐标系．
（1）分别写出直线l1与曲线C的极坐标方程；
（2）若直线${l_2}：2ρsin（θ+\frac{π}{3}）+3\sqrt{3}$=0，直线l1与曲线C的交点为A，直线l1与l2的交点为B，求|AB|．
20．已知函数f（x）=x2+$\frac{a}{x}$，则“0＜a＜2”是“函数f（x）在（1，+∞）上为增函数”的（　　）
A．充分而不必要条件B．必要而不充分条件
C．充要条件D．既不充分也不必要条件
10．某几何体的三视图如图所示，则该几何体的体积为（　　）
A．24B．48C．54D．72
17．已知$sin（α-\frac{π}{12}）=\frac{1}{3}$，则$cos（α+\frac{17π}{12}）$的值等于（　　）
A．$\frac{1}{3}$B．$\frac{{2\sqrt{2}}}{3}$C．$-\frac{1}{3}$D．$-\frac{{2\sqrt{2}}}{3}$
14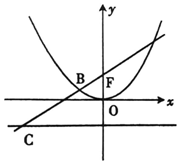．如图，过抛物线x2=2py（p＞0）的焦点F的直线l交抛物线于AB，交其准线于点C，若|BC|=2|BF|，且|AF|=2，则p=（　　）
A．1B．$\sqrt{2}$C．2D．2-$\sqrt{2}$
14．给出下列命题：
①若函数y=f（x）满足f（x-1）=f（x+1），则函数f（x）的图象关于直线x=1对称；
②点（2，1）关于直线x-y+1=0的对称点为（0，3）；
③通过回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$可以估计和观测变量的取值和变化趋势；
④正弦函数是奇函数，f（x）=sin（x2+1）是正弦函数，所以f（x）=sin（x2+1）是奇函数，上述推理错误的原因是大前提不正确．
其中真命题的序号是②③．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网