题目内容
12.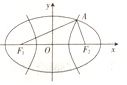 如图F1,F2是双曲线${C_1}:{x^2}-\frac{y^2}{8}=1$与椭圆C2的公共焦点,点A是C1,C2在第一象限内的公共点,若|F1F2|=|F1A|,则C2的离心率是( )
如图F1,F2是双曲线${C_1}:{x^2}-\frac{y^2}{8}=1$与椭圆C2的公共焦点,点A是C1,C2在第一象限内的公共点,若|F1F2|=|F1A|,则C2的离心率是( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{5}$ |
分析 利用椭圆以及双曲线的定义,转化求解椭圆的离心率即可.
解答 解:由题意F1,F2是双曲线${C_1}:{x^2}-\frac{y^2}{8}=1$与椭圆C2的公共焦点可知,|F1F2|=|F1A|=6,
∵|F1A|-|F2A|=2,∴|F2A|=4,∴|F1A|+|F2A|=10,
∵2a=10,∴C2的离心率是$\frac{6}{10}=\frac{3}{5}$.
故选:C.
点评 本题考查椭圆以及双曲线的简单性质的应用,考查计算能力.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
3.已知偶函数f(x)的定义域为(-1,0)∪(0,1),且$f(\frac{1}{e})=0$.当0<x<1时,(1-x2)ln(1-x2)f'(x)>2xf(x),则满足f(x)<0的x的取值范围是( )
| A. | $(-\frac{1}{e},0)∪(0,\frac{1}{e})$ | B. | $(-\frac{1}{2},0)∪(\frac{1}{2},1)$ | C. | $(-1,-\frac{1}{e})∪(\frac{1}{e},1)$ | D. | $(-1,-\frac{1}{2})∪(0,\frac{1}{2})$ |
20.已知函数f(x)=x2+$\frac{a}{x}$,则“0<a<2”是“函数f(x)在(1,+∞)上为增函数”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
7.已知函数f(x)=$\left\{\begin{array}{l}{10x-1,x≤0}\\{{e}^{x},x>0}\end{array}\right.$(e为自然对数的底).若函数g(x)=f(x)-kx恰好有两个零点,则实数k的取值范围是( )
| A. | (1,e) | B. | (e,10] | C. | (1,10] | D. | (10,+∞) |
17.已知$sin(α-\frac{π}{12})=\frac{1}{3}$,则$cos(α+\frac{17π}{12})$的值等于( )
| A. | $\frac{1}{3}$ | B. | $\frac{{2\sqrt{2}}}{3}$ | C. | $-\frac{1}{3}$ | D. | $-\frac{{2\sqrt{2}}}{3}$ |
1.下列命题中不正确的是( )
| A. | 如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥γ | |
| B. | 如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β | |
| C. | 如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β | |
| D. | 如果平面α⊥平面β,且直线l∥平面α,则直线l⊥平面β |
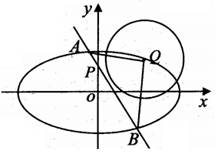 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,圆Q:x2+y2-4x-2y+3=0的圆心Q在椭圆C上,点P(0,1)到椭圆C的右焦点的距离为2.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,圆Q:x2+y2-4x-2y+3=0的圆心Q在椭圆C上,点P(0,1)到椭圆C的右焦点的距离为2.