题目内容
已知各项均不为零的数列{an},定义向量
=(an,an+1),
=(n,n+1),n∈N*.下列命题中真命题是( )
| cn |
| bn |
A、若?n∈N*总有
| ||||||||||||
B、若?n∈N*总有
| ||||||||||||
C、若
| ||||||||||||
D、若?n∈N*总有
|
考点:平面向量数量积的运算
专题:等差数列与等比数列,平面向量及应用
分析:根据题意,分析平面向量平行、垂直的坐标表示,判断数列{an}是否为等差或等比数列.
解答:
解:∵向量
=(an,an+1),
=(n,n+1),n∈N*;
∴当
∥
,(n+1)an-nan+1=0,
即
=
;
∴an=
•
•
•…•
•a1
=
•
•…•
•a1
=na1,
∴数列{an}为等差数列,
∴A正确,B错误;
当
⊥
时,nan+(n+1)an+1=0,
即
=-
;
∴an=
•
•
•…•
•a1
=-
•(-
)•(-
)…(-
)•a1
=
•a1;
∴数列{an}既不是等差数列,也不是等比数列,
∴C、D错误;
故选:A.
| cn |
| bn |
∴当
| cn |
| bn |
即
| an+1 |
| an |
| n+1 |
| n |
∴an=
| an |
| an-1 |
| an-1 |
| an-2 |
| an-2 |
| an-3 |
| a2 |
| a1 |
=
| n |
| n-1 |
| n-1 |
| n-2 |
| 2 |
| 1 |
=na1,
∴数列{an}为等差数列,
∴A正确,B错误;
当
| cn |
| bn |
即
| an+1 |
| an |
| n |
| n+1 |
∴an=
| an |
| an-1 |
| an-1 |
| an-2 |
| an-2 |
| an-3 |
| a2 |
| a1 |
=-
| n-1 |
| n |
| n-2 |
| n-1 |
| n-3 |
| n-2 |
| 1 |
| 2 |
=
| (-1)n-1 |
| n |
∴数列{an}既不是等差数列,也不是等比数列,
∴C、D错误;
故选:A.
点评:本题考查了平面向量平行的坐标表示,也考查了等差与等比数列的应用问题,中档题目.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
数列{an}满足:a1a2a3…an=
,则a2013=( )
| 1 |
| n |
A、
| ||
B、
| ||
C、
| ||
D、
|
若n为奇数,8n-Cn18n-1+Cn28n-2-…+Cnn-18被6除所得的余数是( )
| A、0 | B、1 | C、2 | D、3 |
判定下列命题
①第一象限的角为锐角
②f(x)=xcosx为奇函数
③
-
=
④(
•
)•
=
•(
•
)
正确的为( )
①第一象限的角为锐角
②f(x)=xcosx为奇函数
③
| AB |
| AC |
| CB |
④(
| a |
| b |
| c |
| a |
| b |
| c |
正确的为( )
| A、①② | B、①③ | C、②③ | D、①④ |
统计假设H0:P(AB)=P(A)P(B)成立时,有以下判断:
①P(
B)=P(
)P(B)
②P(A
)=P(A)P(
)
③P(
)=P(
)P(
)
其中真命题个数是( )
①P(
. |
| A |
. |
| A |
②P(A
. |
| B |
. |
| B |
③P(
. |
| A |
. |
| B |
. |
| A |
. |
| B |
其中真命题个数是( )
| A、0 | B、1 | C、2 | D、3 |
设f(x)=
x3+ax2+5x+6在区间[1,3]上单调函数,则实数a的取值范围为( )
| 1 |
| 3 |
A、[-
| ||
| B、(-∞,-3] | ||
C、[-3,
| ||
D、(-∞,-3]∪[-
|
已知实数a,b满足a2+b2=1,则a4+ab+b4的最小值为( )
A、-
| ||
| B、0 | ||
| C、1 | ||
D、
|
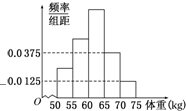 如图是某学校抽取的学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为10,则抽取的学生人数为( )
如图是某学校抽取的学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为10,则抽取的学生人数为( ) 已知E、F、G、H分别是四面体ABCD的棱AD、CD、BD、BC的中点.求证:AH∥平面EFG.
已知E、F、G、H分别是四面体ABCD的棱AD、CD、BD、BC的中点.求证:AH∥平面EFG.