题目内容
16.设M(p,0)是一定点,0<p<1,点A(a,b)是椭圆$\frac{{x}^{2}}{4}$+y2=1距离M最近的点,则a=f(p)=$\frac{4p}{3}$.分析 设A(2cosα,sinα)0<α<π,根据题意AM2=(2cosα-p)2+sin2α,换元,利用配方法,即可得出结论.
解答 解:椭圆方程$\frac{{x}^{2}}{4}$+y2=1,那么a=2,b=1
设A(2cosα,sinα)0<α<π,根据题意AM2=(2cosα-p)2+sin2α.
令y=(2cosα-p)2+sin2α=4cos2α-4pcosα+p2+sin2α=3cos2α-4pcosα+p2+1
令t=cosα,-1≤t≤1,y=3t2-4pt+p2+1=3(t-$\frac{2p}{3}$)2+1-$\frac{{p}^{2}}{3}$
∵0<p<1,0<$\frac{2p}{3}$<$\frac{2}{3}$,
当t=$\frac{2p}{3}$时,y有最小值1-$\frac{{p}^{2}}{3}$
此时cosα=$\frac{2p}{3}$,∴a=2cosα=$\frac{4p}{3}$.
故答案为:$\frac{4p}{3}$.
点评 本题考查椭圆的参数方程,考查距离公式,考查配方法的运用,属于中档题.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
7.在空间四边形OABC中,G是△ABC的重心,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{OG}$=( )
| A. | $\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$ | B. | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$ | C. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$ | D. | 3$\overrightarrow{a}$+3$\overrightarrow{b}$+3$\overrightarrow{c}$ |
11.从一个正方体中截去部分几何体,得到的剩余几何体的三视图如图,则此几何体的体积是( )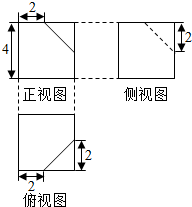

| A. | 64 | B. | $\frac{122}{3}$ | C. | $\frac{188}{3}$ | D. | $\frac{47}{6}$ |